题目内容
17.下列事件中,必然事件是( )| A. | 抛掷一枚硬币,四次中有两次正面朝上 | |
| B. | 打开电视正在播放NBA球赛 | |
| C. | 在标准大气压下,温度低于0℃时冰融化 | |
| D. | 367人中有两人生日相同 |
分析 A:抛掷一枚硬币,四次中不一定有几次正面朝上,所以四次中有两次正面朝上是随机事件,据此判断即可.
B:打开电视可能正在播放NBA球赛,也可能不在播放NBA球赛,所以打开电视正在播放NBA球赛是随机事件,据此判断即可.
C:在标准大气压下,温度低于0℃时冰融化是确定事件中的不可能事件,据此判断即可.
D:根据一年最多有366天,可得每个人的生日最多有366种情况,所以367人中一定有两人生日相同,所以367人中有两人生日相同是必然事件,据此判断即可.
解答 解:∵抛掷一枚硬币,四次中不一定有几次正面朝上,
∴四次中有两次正面朝上是随机事件,
∴选项A不正确;
∵打开电视可能正在播放NBA球赛,也可能不在播放NBA球赛,
∴打开电视正在播放NBA球赛是随机事件,
∴选项B不正确;
∵在标准大气压下,温度低于0℃时冰融化是确定事件中的不可能事件,
∴选项C不正确;
∵一年最多有366天,
∴每个人的生日最多有366种情况,
∴367人中一定有两人生日相同,
∴367人中有两人生日相同是必然事件,
∴选项D正确.
故选:D.
点评 此题主要考查了随机事件的含义和分类,要熟练掌握,解答此题的关键是要明确:事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若|a|=2,|b|=5,则|a-b|的值等于( )
| A. | 3 | B. | 7 | C. | -7 | D. | 3或7 |
5.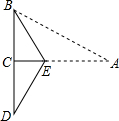 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
2.已知一元二次方程ax2+bx+c=0(a≠0)中,下列命题是真命题的有( )
①若a+b+c=0,则b2-4ac≥0
②若方程ax2+bx+c=0两根为1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根.
①若a+b+c=0,则b2-4ac≥0
②若方程ax2+bx+c=0两根为1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
9.计算(-3)-(-5)的结果等于( )
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |
7.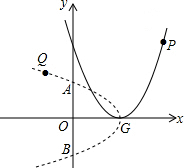 如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
 如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )
如图,点P为抛物线y=x2-4x+4上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.若点P的横坐标为4时,则Q点的坐标为( )| A. | (-2,3) | B. | (-2,2$\sqrt{2}$) | C. | (-2,2) | D. | (1+$\frac{\sqrt{2}}{2}$,2) |