题目内容
a，b，c三个数在数轴上的位置如图所示，化简|a+b|-|b-c|+|c-a|-|a-b|=
考点：整式的加减,数轴,绝对值
专题：
分析：根据数轴点的位置得出a+b＜0，b-c＜0，c-a＞0，a-b＜0，再去掉绝对值符号，合并同类项即可．
解答：解：∵从数轴可知：a＜b＜0＜c，|b|＜|c|，
∴a+b＜0，b-c＜0，c-a＞0，a-b＜0，
∴|a+b|-|b-c|+|c-a|-|a-b|=
=-（a+b）-（c-b）+（c-a）-（b-a）
=-a-b-c+b+c-a-b+a
=-a-b，
故答案为：-a-b．
∴a+b＜0，b-c＜0，c-a＞0，a-b＜0，
∴|a+b|-|b-c|+|c-a|-|a-b|=
=-（a+b）-（c-b）+（c-a）-（b-a）
=-a-b-c+b+c-a-b+a
=-a-b，
故答案为：-a-b．
点评：本题考查了整式的加减和数轴的应用，解此题的关键是能根据数轴去掉绝对值符号，题目比较好，难度不是很大．
练习册系列答案
相关题目
下列运算中，计算结果正确的是（ ）
| A、a2•a3=a6 |
| B、（a2）3=a5 |
| C、（-2xy）2=-6x3y3 |
| D、a3+a3=2a3 |
如图，在△ABC中，∠ACB=90°，∠B=40°，AE平分∠BAC，AC的垂直平分线DE分别与AC、AE交于点D、E，那么∠BCE=下列运算中，正确的是（ ）
| A、a•a2=a2 |
| B、（x+2）2=x2+4 |
| C、（ab3）2=ab6 |
| D、（-1）0=1 |
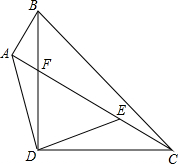如图，以Rt△ABC的斜边BC为斜边在△ABC的同侧作等腰Rt△BCD，连接AD，过D作DE⊥AD交AC于E，AB=1，AD=