题目内容
【题目】如图,地物线点![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 均不为0)的顶点为
均不为0)的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,我们称以
,我们称以![]() 为顶点,对称轴是
为顶点,对称轴是![]() 轴且过点
轴且过点![]() 的抛物线为抛物线
的抛物线为抛物线![]() 的衍生抛物线,直线
的衍生抛物线,直线![]() 为抛物线
为抛物线![]() 的衍生直线.
的衍生直线.
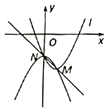
(1)求抛物线![]() 的衍生抛物线和衍生直线的解析式;
的衍生抛物线和衍生直线的解析式;
(2)若一条抛物线的衍生抛物线和衍生直线分别是![]() 和
和![]() ,求这条抛物线的解析式.
,求这条抛物线的解析式.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
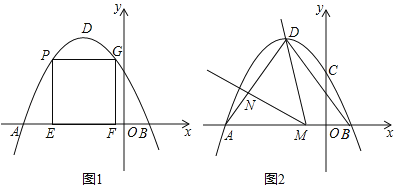
(1)衍生抛物线顶点为原抛物线与y轴的交点,则可根据顶点设顶点式方程,由衍生抛物线过原抛物线的顶点代入顶点坐标可求出衍生抛物线解析式.根据衍生直线经过M、N可求衍生直线的解析式.
(2)已知衍生抛物线和衍生直线求原抛物线思路正好与(1)相反,根据衍生抛物线与衍生直线的两交点分别为衍生抛物线与原抛物线的交点,则可推得原抛物线顶点式,再代入经过点,即得解析式.
解:(1)∵抛物线![]() 点过
点过![]() ,
,
∴设其衍生抛物线为![]() .
.
∵![]() ,
,
∴衍生抛物线![]() 过抛物线
过抛物线![]() 的顶点
的顶点![]() .
.
∴![]() ,即
,即![]() .
.
∴衍生抛物线为![]() .
.
设衍生直线为![]() ,则直线
,则直线![]() 点过
点过![]() 与
与![]() ,
,
∴![]() 解得
解得![]()
∴衍生直线为![]() .
.
(2)∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点,
∴将![]() 和
和![]() 联立,得
联立,得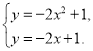
解得![]() 或
或![]()
∵衍生抛物线![]() 的顶点为
的顶点为![]() ,
,
∴原抛物线的顶点为![]() .
.
设原抛物线为![]() ,则抛物线
,则抛物线![]() 过点
过点![]() ,
,
∴![]() ,即
,即![]() ,
,
∴原抛物线为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目