题目内容
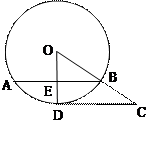
如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD= .
.求:(1)弦AB的长;
(2)CD的长;
(3)线段DE、线段BE与弧DB围成的面积.

【答案】分析:(1)sin∠COD= ,可得∠COD=60°,由弦AB⊥OD,根据三角函数的性质与垂径定理,即可求得弦AB的长;
,可得∠COD=60°,由弦AB⊥OD,根据三角函数的性质与垂径定理,即可求得弦AB的长;
(2)由CD切⊙O于点D,可得OD⊥CD,继而求得CD的长;
(3)由S=S扇形BOD-S△BOE,即可求得答案.
解答:解:(1)∵sin∠COD= ,
,
∴∠COD=60°,
∵弦AB⊥OD,⊙O的半径为15,
∴AE=BE=OB•sin60°=15× =
=
 ,
,
∴AB=AE+BE=15 ;
;
(2)∵CD切⊙O于点D,
∴OD⊥CD,
在Rt△OCD中,OD=15,∠COD=60°,
∴CD=OD•tan60°=15× =15
=15 ;
;
(3)在Rt△OBE中,OE=OB•cos60°=15× =
= ,
,
S=S扇形BOD-S△BOE= ×π×152-
×π×152- ×
× ×
× =25π-
=25π- .
.
点评:此题考查了切线的性质、垂径定理、扇形的面积以及三角函数的性质.此题难度不大,注意掌握数形结合思想的应用.
 ,可得∠COD=60°,由弦AB⊥OD,根据三角函数的性质与垂径定理,即可求得弦AB的长;
,可得∠COD=60°,由弦AB⊥OD,根据三角函数的性质与垂径定理,即可求得弦AB的长;(2)由CD切⊙O于点D,可得OD⊥CD,继而求得CD的长;
(3)由S=S扇形BOD-S△BOE,即可求得答案.
解答:解:(1)∵sin∠COD=
 ,
,∴∠COD=60°,
∵弦AB⊥OD,⊙O的半径为15,
∴AE=BE=OB•sin60°=15×
 =
=
 ,
,∴AB=AE+BE=15
 ;
;(2)∵CD切⊙O于点D,
∴OD⊥CD,
在Rt△OCD中,OD=15,∠COD=60°,
∴CD=OD•tan60°=15×
 =15
=15 ;
;(3)在Rt△OBE中,OE=OB•cos60°=15×
 =
= ,
,S=S扇形BOD-S△BOE=
 ×π×152-
×π×152- ×
× ×
× =25π-
=25π- .
.点评:此题考查了切线的性质、垂径定理、扇形的面积以及三角函数的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 in∠COD=
in∠COD=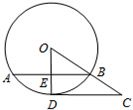 10,sin∠COD=
10,sin∠COD= 如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=
如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=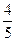 .
.