题目内容
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
(1)如果木棍的顶端A沿墙下滑0.4米,那么木棍的底端B向外移动多少距离?
(2)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.

解:(1)在直角△ABC中,已知AB=2.5m,BO=0.7m,
则由勾股定理得:AO= =2.4m,
=2.4m,
∴OC=2m,
∵直角三角形CDO中,AB=CD,且CD为斜边,
∴由勾股定理得:OD= =1.5m,
=1.5m,
∴BD=OD﹣OB=1.5m﹣0.7m=0.8m;
(2)不变.
理由:在直角三角形中,斜边上的中线等于斜边的一半,因为斜边AB不变,所以斜边上的中线OP不变;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (
(
 ,a、b为两个连续的整数,
,a、b为两个连续的整数, <
< <
< ,
,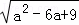 +|b﹣4|=0,
+|b﹣4|=0, +|b﹣4|=0,
+|b﹣4|=0,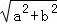 =
=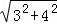 =5.
=5.
 )□(﹣
)□(﹣ 与-5互为相反数,则
与-5互为相反数,则