题目内容
(本题满分9分)如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y= x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.

(1)求证:△ADO≌△AEC;
(2)求AP的长.
(1)见解析;(2)AP=20.
【解析】
试题分析:根据图先求出D、E的坐标,然后再根据全等三角形的判定定理即可得出结论;
(2)由(1)的结论,即可得出∠DAE=90°,再由勾股定理得出DE的长,然后利用中点的性质即可得出AP的值.
试题解析:
(1) 由题意可得:D(—4,0),E(28,24)
在△ADO与△AEC中

∴△ADO≌△AEC.
由△ADO≌△AEC全等可知:∠EAC=∠DAO,
∴∠DAE=90°.
∵P为DE中点,
∴AP= DE
DE
在Rt△DBE中,DE2=BD2+BE2=242+322=1600
∴DE=40,
∴AP=20.
考点:全等三角形的性质和判定;勾股定理.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目

 ,则底角为 .
,则底角为 .
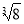 +
+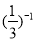 -
-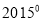 ; (2)已知:(x-1)2=9,求x的值.
; (2)已知:(x-1)2=9,求x的值. 的值是( )
的值是( ) -2 B.0 C.2
-2 B.0 C.2 ,AD=1.求BC的长.
,AD=1.求BC的长.