题目内容
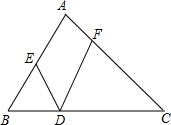 如图所示,在△ABC中,点D、E、F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为( )
如图所示,在△ABC中,点D、E、F分别在BC、AB、AC上,且BD=BE,CD=CF,∠EDF=50°.则∠A的度数为( )| A、65° | B、80° |
| C、40° | D、30° |
考点:等腰三角形的性质,三角形内角和定理
专题:计算题,整体思想
分析:由∠EDF=50°可得∠BDE+∠CDF=130°,根据三角形内角和定理可求出∠B+∠C,就可求出∠A.
解答:解:∵BD=BE,CD=CF,
∴∠BDE=∠BED,∠CDF=∠CFD.
∵∠BDE+∠EDF+∠CDF=180°,∠EDF=50°,
∴∠BDE+∠CDF=130°.
∵∠B+∠BDE+∠BED=180°,∠C+∠CDF+∠CFD=180°,
∴∠B+∠BDE+∠BED+∠C+∠CDF+∠CFD=360°.
∴∠B+∠C+2∠BDE+2∠CDF=360°.
∴∠B+∠C+260°=360°.
∴∠B+∠C=100°.
∵∠A+∠B+∠C=180°,
∴∠A=80°.
故选:B.
∴∠BDE=∠BED,∠CDF=∠CFD.
∵∠BDE+∠EDF+∠CDF=180°,∠EDF=50°,
∴∠BDE+∠CDF=130°.
∵∠B+∠BDE+∠BED=180°,∠C+∠CDF+∠CFD=180°,
∴∠B+∠BDE+∠BED+∠C+∠CDF+∠CFD=360°.
∴∠B+∠C+2∠BDE+2∠CDF=360°.
∴∠B+∠C+260°=360°.
∴∠B+∠C=100°.
∵∠A+∠B+∠C=180°,
∴∠A=80°.
故选:B.
点评:本题考查了等腰三角形的性质、三角形的内角和定理、平角的定义等知识,考查了整体思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
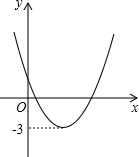 二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )| A、k>-3 | B、k<-3 |
| C、k=-3 | D、无法确定 |
已知甲乙两个样本,如果甲的样本方差为0.4,乙的样本方差为0.6,那么( )
| A、甲的波动比乙的大 |
| B、乙的波动比甲的大 |
| C、甲、乙波动一样大 |
| D、无法确定 |
下列说法错误的是( )
| A、在频数分布直方图中,频数之和为数据个数 |
| B、频率等于频数与组距的比值 |
| C、在频数分布表中,频率之和为1 |
| D、频率等于频数与样本容量的比值 |
下列图形中,由∠1=∠2≠90°,能得到AB∥CD的是( )
A、 |
B、 |
C、 |
D、 |