题目内容
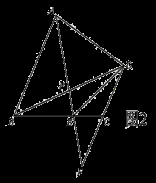
(本题8分)如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.
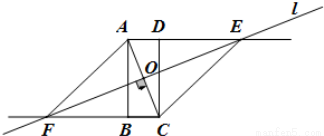
(1)△ABC与△FOA相似吗?为什么?
(2)试判定四边形AFCE的形状,并说明理由.
(1)△ABC∽△FOA,理由详见解析;(2)四边形AFCE是菱形,理由详见解析.
【解析】
试题分析:(1)根据垂直平分线的定义,同角的余角相等可知∠AFO=∠CAB,根据垂直的定义,矩形的性质可知∠ABC=∠FOA,由相似三角形的判定可证△ABC与△FOA相似;
(2)先证明四边形AFCE是平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判断.
试题解析:(1)△ABC∽△FOA,理由如下:
因为直线l垂直平分线段AC,所以∠AFO=∠CFO,因为∠CFO+∠FCO=∠CAB+∠FCO=90°,所以∠AFO=∠CAB,因为∠ABC=∠FOA=90°,所以△ABC∽△FOA.
(2)四边形AFCE是菱形,理由如下:
由(1)知△ABC∽△FOA,所以∠ACB=∠FAC,因为AD∥BC,所以∠ACB=∠EAC,所以∠FAC=∠EAC,在△AOF与△AOE中,∠FAC=∠EAC,AO=AO,∠AOF=∠AOE,所以△AOF≌△AOE,所以AE=AF,OE=OF,因为AD∥BC,AD=BC,所以四边形AFCE是平行四边形,所以四边形AFCE是菱形.
考点:矩形的性质;菱形的判定;相似三角形的判定和性质;全等三角形的判定和性质.
考点分析: 考点1:图形的相似 形状相同,大小不同的两个图形相似 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,则a+b+c+d的值为 .
,则a+b+c+d的值为 .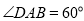 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
 B.10 C.4 D.2
B.10 C.4 D.2
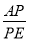 的值;
的值;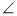 BAE=
BAE=

