题目内容
【题目】若一个三角形一条边的平方等于另两条的乘积，我们把这个三角形叫做比例三角形．
（1）已知
是比例三角形，
，
，请直接写出所有满足条件的
的长；
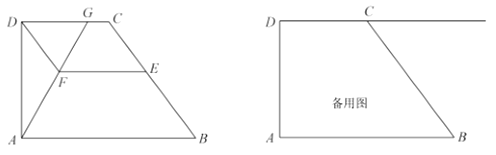
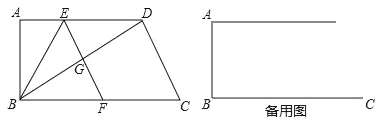
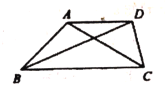
（2）如图，在四边形
中，
，对角线
平分
，
．求证：是比例三角形；
【答案】（1）当AC=
或
或
时，△ABC是比例三角形；（2）见解析
【解析】
（1）根据比例三角形的定义，分AB2=BCAC、BC2=ABAC、AC2=ABBC三种情况分别代入计算可得；
（2）先证△ABC∽△DCA得CA2=BC·AD，再由∠ADB=∠CBD=∠ABD知AB=AD即可得．
（1）∵△ABC是比例三角形，且AB=2、BC=3，
①当AB2=BC·AC时，得：4=3AC，解得：AC=；
②当BC2=AB·AC时，得：9=2AC，解得：AC=；
③当AC2=AB·BC时，得：AC2=6，解得：AC=（负值舍去）；
所以当AC=或或时，△ABC是比例三角形；．
（2）∵AD//BC，
∴∠ACB=∠CAD，
又∵∠BAC=∠ADC，
∴△ABC∽△DCA，
∴
，即CA2=BC·AD，
∵AD∥BC，
∴∠ADB=∠CBD，
∵BD平分∠ABC，
∴∠ABD=∠CBD，
∴∠ADB=∠ABD，
∴AB=AD，
∴CA2=BC·AB，
∴△ABC是比例三角形．
练习册系列答案
相关题目
