МвДүДЪИЭ
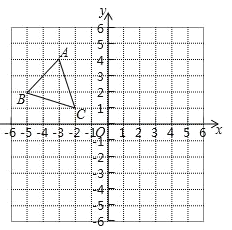
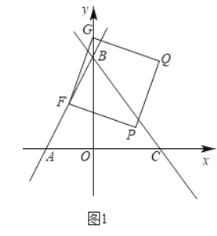
ҰңМвДүҰүИзНәӘ¬ФЪЖҢГжЦ±ҢЗЧш±кПµЦРӘ¬Ц±ПЯ![]() УлxЦбҢ»УЪµгAӘ¬УлyЦбҢ»УЪµгBӘ¬№эµгBµДЦ±ПЯҢ»xЦбУЪCӘ¬ЗТ
УлxЦбҢ»УЪµгAӘ¬УлyЦбҢ»УЪµгBӘ¬№эµгBµДЦ±ПЯҢ»xЦбУЪCӘ¬ЗТ![]() Гж»эОҒ10.
Гж»эОҒ10.
ӘЁ1Ә©ЗуµгCµДЧш±кә°Ц±ПЯBCµДҢвОцКҢӘ»
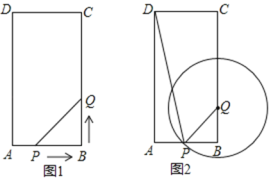
ӘЁ2Ә©ИзНә1Ә¬ЙиµгFОҒПЯ¶ОABЦРµгӘ¬µгGОҒyЦбЙПТ»¶ҮµгӘ¬Б¬ҢУFGӘ¬ТФFGОҒ±ЯПтFGУТІаЧчХэ·ҢРОFGQPӘ¬ФЪGµгµДФЛ¶Ү№эіМЦРӘ¬µ±¶ӨµгQВдФЪЦ±ПЯBCЙПК±Ә¬ЗуµгGµДЧш±кӘ»
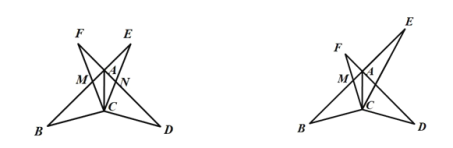
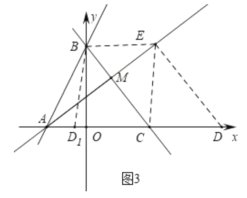
ӘЁ3Ә©ИзНә2Ә¬ИфMОҒПЯ¶ОBCЙПТ»µгӘ¬ЗТВъЧг![]() Ә¬µгEОҒЦ±ПЯAMЙПТ»¶ҮµгӘ¬ФЪxЦбЙПКЗ·сөжФЪµгDӘ¬К№ТФµгDҰұEҰұBҰұCОҒ¶ӨµгµДЛД±ЯРООҒЖҢРРЛД±ЯРОӘүИфөжФЪӘ¬ЗлЦ±ҢУРөіцµгDµДЧш±кӘ»ИфІ»өжФЪӘ¬ЗлЛµГчАнУЙ.
Ә¬µгEОҒЦ±ПЯAMЙПТ»¶ҮµгӘ¬ФЪxЦбЙПКЗ·сөжФЪµгDӘ¬К№ТФµгDҰұEҰұBҰұCОҒ¶ӨµгµДЛД±ЯРООҒЖҢРРЛД±ЯРОӘүИфөжФЪӘ¬ЗлЦ±ҢУРөіцµгDµДЧш±кӘ»ИфІ»өжФЪӘ¬ЗлЛµГчАнУЙ.

Ұңөр°ёҰүӘЁ1Ә©C(3,0)Ә»y=![]() Ә»ӘЁ2Ә©GµгЧш±кОҒG(0,
Ә»ӘЁ2Ә©GµгЧш±кОҒG(0,![]() ),G(0,
),G(0,![]() )Ә»ӘЁ3Ә©DµгЧш±кОҒ(
)Ә»ӘЁ3Ә©DµгЧш±кОҒ(![]() ,0)»т (
,0)»т (![]() ,0) »т(
,0) »т(![]() ,0)
,0)
ҰңҢвОцҰү
ӘЁ1Ә©АыУГИэҢЗРОГж»э№«КҢЗуіцµгCЧш±кӘ¬ФЩАыУГөэ¶ЁПµКэ·ЁЗуҢвОцКҢәөүЙӘ»
ӘЁ2Ә©·ЦБҢЦЦЗйүцӘғұЩµ±nӘң2К±Ә¬ИзНә2-1ЦРӘ¬µгQВдФЪBCЙПӘ¬№эGµгЧчЦ±ПЯЖҢРРУЪxЦбӘ¬№эµгFҰұQЧчёГЦ±ПЯµДө№ПЯӘ¬ө№Чг·Ц±рОҒMҰұNӘ¬ЗуіцQ(n-2Ә¬n-1).ұЪµ±nӘә2К±Ә¬ИзНә2-2Ә¬Н¬АнүЙµГQ(2-nӘ¬n+1)Ә¬АыУГөэ¶ЁПµКэ·ЁЗуҢвәөүЙӘ»
ӘЁ3Ә©АыУГИэҢЗРОГж»э№«КҢЗуіцMЧш±кӘ¬өУ¶шЗуіцЦ±ПЯAMµДҢвОцКҢӘ¬ЧчBEҰОOCҢ»AMУЪEӘ¬µ±CD=BEК±үЙµГЛД±ЯРОBCDEӘ¬ЛД±ЯРОBECD1КЗЖҢРРЛД±ЯРОӘ¬И»ғуҢшТ»ІҢµГіцёчµгЧш±к.
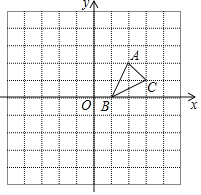
ӘЁ1Ә©ҰЯЦ±ПЯy=2x+4УлxЦбҢ»УЪµгAӘ¬УлyЦбҢ»УЪµгBӘ¬
ҰаA(-2,0)Ә¬B(0,4)Ә¬
ҰаOA=2Ә¬OB=4Ә¬
ҰЯSҰчABC=![]() ACOB=10Ә¬
ACOB=10Ә¬
ҰаAC=5Ә¬
ҰаOC=3Ә¬
ҰаC(3,0)Ә¬
ЙиЦ±ПЯBCҢвОцКҢОҒy=kx+bӘ¬
ФтӘғ3k+b=0Ә¬b=4Ә¬
Ұаk=![]() Ә¬
Ә¬
ҰаЦ±ПЯBCҢвОцКҢОҒy=![]() Ә»
Ә»
ӘЁ2Ә©ҰЯFA=FBӘ¬A(-2,0)Ә¬B(0,4)Ә¬
ҰаF(-1,2)Ә¬ЙиG(0,n)Ә¬
µ±nӘң2К±Ә¬ИзНә2-1ЛщКңӘ¬µгQВдФЪBCЙПК±Ә¬№эGЧчЦ±ПЯЖҢРРУЪxЦбӘ¬№эµгFҰұQЧчёГЦ±ПЯµДө№ПЯӘ¬ө№Чг·Ц±рОҒMҰұNӘ¬
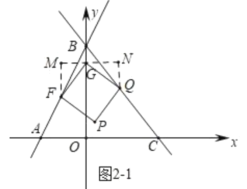
ҰЯЛД±ЯРОFGQPКЗХэ·ҢРОӘ¬
ҰаҰчFMGҰХҰчGNQӘ¬
ҰаMG=NQ=1Ә¬FM=GN=n-2Ә¬
ҰаQ(n-2Ә¬n-1)Ә¬
ҰЯQµгФЪЦ±ПЯy=![]() ЙПӘ¬
ЙПӘ¬
Ұаn-1=![]() Ә¬
Ә¬
Ұаn=![]() Ә¬
Ә¬
ҰаG(0,![]() ),
),
µ±nӘә2К±Ә¬ИзНә2-2Ә¬Н¬АнүЙµГӘғQ(2-nӘ¬n+1)Ә¬

ҰЯQµгФЪЦ±ПЯy=![]() ЙПӘ¬
ЙПӘ¬
Ұаn+1=![]() Ә¬
Ә¬
Ұаn=![]() Ә¬
Ә¬
ҰаG(0,![]() ),
),
ЧЫЙПЛщКцӘ¬GµгЧш±кОҒG(0,![]() ),G(0,
),G(0,![]() )Ә»
)Ә»
ӘЁ3Ә©ИзНә3Ә¬ЙиM(m,![]() )Ә¬
)Ә¬
ҰЯ![]() Ә¬
Ә¬
Ұа![]() Ә¬
Ә¬
Ұа![]() Ә¬
Ә¬
ҢвµГ![]() Ә¬
Ә¬
ҰаM(![]() ,
,![]() )Ә¬
)Ә¬
ҰаЦ±ПЯAMµДҢвОцКҢОҒ![]() Ә¬
Ә¬
ЧчBEҰОOCҢ»Ц±ПЯAMУлEӘ¬өЛК±E(![]() ,4)Ә¬
,4)Ә¬
µ±CD=BEК±Ә¬ЛД±ЯРОBCDEӘ¬ЛД±ЯРОBECD1КЗЖҢРРЛД±ЯРОӘ¬
үЙµГӘғD(![]() ,0)Ә¬D1(
,0)Ә¬D1(![]() ,0)Ә¬
,0)Ә¬
ёщңЭ¶ФіЖРФүЙµГD№ШУЪAµД¶ФіЖµгD2(![]() ,0)ТІ·ығПМхәюӘ¬
,0)ТІ·ығПМхәюӘ¬
ЧЫЙПЛщКцӘ¬DµгЧш±кОҒӘғ(![]() ,0)»т (
,0)»т (![]() ,0) »т(
,0) »т(![]() ,0)
,0)