Question

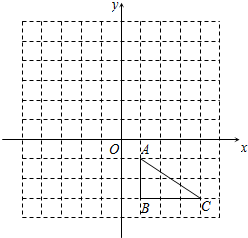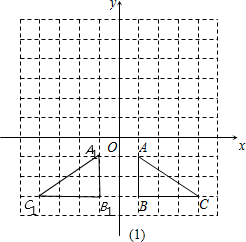
如图，△ABC中，A（1，-1）、B（1，-3）、C（4，-3）．
（1）△A₁B₁C₁是△ABC关于y轴的对称图形，则点A的对称点A₁的坐标是

 

；
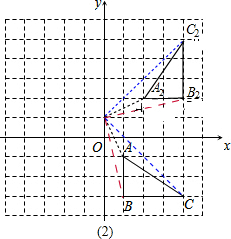
（2）将△ABC绕点（0，1）逆时针旋转90°得到△A₂B₂C₂，则B点的对应点B₂的坐标是

 

；
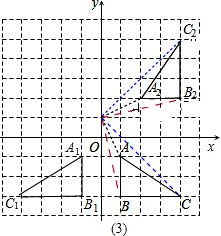
（3）△A₁B₁C₁与△A₂B₂C₂是否关于某条直线成轴对称？若成轴对称，则对称轴的解析式是

 

．

Answer 1

分析：（1）根据轴对称的性质及关于y轴对称的点的坐标特征解答即可．
（2）利用网格，将图形旋转90°，即可得到B₂的坐标．
（3）连接△A₁B₁C₁与△A₂B₂C₂的对应点，对应点连线的垂直平分线即为所求直线．

解答：解：（1）由图可知，A的对应点A₁的坐标为（-1，-1）．
故答案为：（-1，-1）．

（2）由图可知，B₂的坐标为（4，2）；
故答案为：（4，2）．

（3）由图可见，直线过（0，1）和（1，0），
设函数解析式为y=kx+b，
将（0，1）和（1，0）分别代入解析式得，

k+b=0 b=1

，
解得

k=-1 b=1

，
故的函数解析式为y=-x+1．
故答案为：y=-x+1．

点评：此题考查了坐标变化旋转与对称，作出图形，根据对称与旋转的性质找到关键点是解题的关键．