题目内容
如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D
出发,以每秒1个单位长度沿D→C→B向终点B运动,直线EP交AD于点F,过点F作
直线FG⊥DE于点G,交AB于点R。
1.(1)求证:AF=AR;(3分)
2.(2)设点P运动的时间为t,
①求当t为何值时,四边形PRBC是矩形?(4分)
②如图2,连接PB。请直接写出使△PRB是等腰三角形时t的值。(2分)
1.(1)如图3,在正方形ABCD中,AD=AB=2,
 ∵AE=AB
∵AE=AB
∴AD=AE
∴∠AED=∠ADE=45°
又∵FG⊥DE
∴在Rt△EGR中,∠GER=∠GRE=45°
∴在Rt△ARF中,∠FRA=∠GRE=45°
∴∠FRA=∠RFA=45°
∴AF=AR
2.(2)①如图3,当四边形PRBC是矩形时,则有PR∥BC
∴AF∥PR
∴△EAF∽△ERP
∴![]()
即:![]()
由(1)得AF=AR
∴![]()
解得:
![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
∵点P从点D出发,以每秒1个单位长度沿D→C→B向终点B运动
∴![]() (秒)
(秒)
②  (秒)
(秒)
解析:略

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
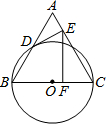 如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF=
如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF=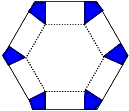 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )