题目内容
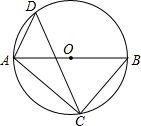 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于( )
如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于( )| A、36° | B、44° |
| C、46° | D、54° |
考点:圆周角定理
专题:
分析:根据直径所对的圆周角等于90°可得∠ACB=90°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等可得∠ABC=54°,然后再计算出∠BAC的度数即可.
解答:解:∵AB为⊙O直径,
∴∠ACB=90°,
∵∠ADC=54°,
∴∠ABC=54°,
∴∠BAC=180°-90°-54°=36°,
故选:A.
∴∠ACB=90°,
∵∠ADC=54°,
∴∠ABC=54°,
∴∠BAC=180°-90°-54°=36°,
故选:A.
点评:此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
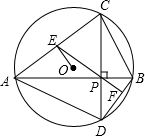 如图,△ABC内接于⊙O,CD⊥AB于P,交⊙O于D,E为AC的中点,EP交BD于F,⊙O的直径为d.下列结论:
如图,△ABC内接于⊙O,CD⊥AB于P,交⊙O于D,E为AC的中点,EP交BD于F,⊙O的直径为d.下列结论:①EF⊥BD;②AC2+BD2的值为定值;③OE=
| 1 |
| 2 |
其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
在平面直角坐标系中,点P(-1,2)关于x轴的对称点的坐标为( )
| A、(-1,-2) |
| B、(1,2) |
| C、(2,-1) |
| D、(-2,1) |
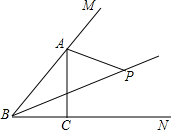 如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
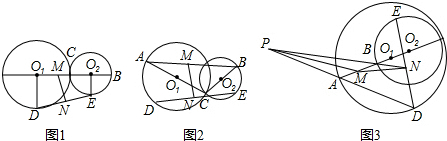
如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上. 如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
 用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.
用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.