题目内容
若∠MON=80°,且OA平分∠MOP,OB平分∠NOP,当射线OP在∠MON外部绕点O旋转时,∠AOB的度数是________.
40°或140°
分析:作边OM、ON的反向延长线OC、OD,然后分①射线OP在∠MOD或∠NOC内部绕点O旋转时,根据角平分线的定义表示出∠AOP和∠BOP,然后根据∠AOB=∠BOP-∠AOP整理,再代入数据计算即可得解;②当射线OP在∠COD的区域绕点O旋转时,根据角平分线的定义表示出∠AOP和∠BOP,然后根据∠AOB=∠BOP+∠AOP整理,再代入数据计算即可得解.
解答: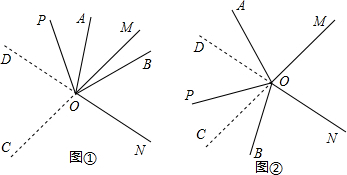 40°或140°.
40°或140°.
作边OM、ON的反向延长线OC、OD,则有如下两种情况:
①当射线OP在∠MOD或∠NOC内部绕点O旋转时,如图①,
∵OA平分∠MOP,
∴∠AOP= ∠MOP,
∠MOP,
∵OB平分∠NOP,
∴∠BOP= ∠NOP,
∠NOP,
∴∠AOB=∠BOP-∠AOP= (∠NOP-∠MOP)=
(∠NOP-∠MOP)= ∠MON,
∠MON,
∵∠MON=80°,
∴∠AOB=40°;
②当射线OP在∠COD的区域绕点O旋转时(如图②),
∵OA平分∠MOP,
∴∠AOP= ∠MOP,
∠MOP,
∵OB平分∠NOP,
∴∠BOP= ∠NOP,
∠NOP,
∴∠AOB=∠AOP+∠BOP= (∠MOP+∠NOP)=
(∠MOP+∠NOP)= (360°-∠MON),
(360°-∠MON),
∵∠MON=80°,
∴∠AOB= (360°-80°)=140°.
(360°-80°)=140°.
综上所述,∠AOB的度数是40°或140°.
故答案为:40°或140°.
点评:本题考查了角的计算,角平分线的定义,注意分射线OP在∠MON的对顶角内和对顶角外两种情况讨论求解.
分析:作边OM、ON的反向延长线OC、OD,然后分①射线OP在∠MOD或∠NOC内部绕点O旋转时,根据角平分线的定义表示出∠AOP和∠BOP,然后根据∠AOB=∠BOP-∠AOP整理,再代入数据计算即可得解;②当射线OP在∠COD的区域绕点O旋转时,根据角平分线的定义表示出∠AOP和∠BOP,然后根据∠AOB=∠BOP+∠AOP整理,再代入数据计算即可得解.
解答:
 40°或140°.
40°或140°.作边OM、ON的反向延长线OC、OD,则有如下两种情况:
①当射线OP在∠MOD或∠NOC内部绕点O旋转时,如图①,
∵OA平分∠MOP,
∴∠AOP=
 ∠MOP,
∠MOP,∵OB平分∠NOP,
∴∠BOP=
 ∠NOP,
∠NOP,∴∠AOB=∠BOP-∠AOP=
 (∠NOP-∠MOP)=
(∠NOP-∠MOP)= ∠MON,
∠MON,∵∠MON=80°,
∴∠AOB=40°;
②当射线OP在∠COD的区域绕点O旋转时(如图②),
∵OA平分∠MOP,
∴∠AOP=
 ∠MOP,
∠MOP,∵OB平分∠NOP,
∴∠BOP=
 ∠NOP,
∠NOP,∴∠AOB=∠AOP+∠BOP=
 (∠MOP+∠NOP)=
(∠MOP+∠NOP)= (360°-∠MON),
(360°-∠MON),∵∠MON=80°,
∴∠AOB=
 (360°-80°)=140°.
(360°-80°)=140°.综上所述,∠AOB的度数是40°或140°.
故答案为:40°或140°.
点评:本题考查了角的计算,角平分线的定义,注意分射线OP在∠MON的对顶角内和对顶角外两种情况讨论求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
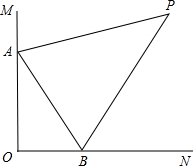 如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.
如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.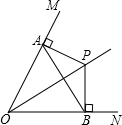 如图,点P是∠MON中一点,PA⊥OM于A,PB⊥ON于B,连接AB,∠PAB=∠PBA.
如图,点P是∠MON中一点,PA⊥OM于A,PB⊥ON于B,连接AB,∠PAB=∠PBA.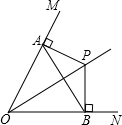 如图,点P是∠MON中一点,PA⊥OM于A,PB⊥ON于B,连接AB,∠PAB=∠PBA.
如图,点P是∠MON中一点,PA⊥OM于A,PB⊥ON于B,连接AB,∠PAB=∠PBA. 如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.
如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.