题目内容
已知：Rt△ABC中，∠ACB=90°，CD⊥AB于D点，AB=2m，BD=m-1，cosA=
．则m=
．
| 4 |
| 5 |
| 25 |
| 7 |
| 25 |
| 7 |
分析：由cosA=
可求出sinB=cosA=
，因为sin2B+cos2B=1，进而求出cosB的值，因为AB=2m，BD=m-1，所以可建立m的方程求出m的值即可．
| 4 |
| 5 |
| 4 |
| 5 |
解答：
解：∵cosA=
，
∴sinB=cosA=
，
∴cosB=
∵
=cosB，
∴BC=
（m-1），
∵AB=2m，
∴BC=
×2m，
∴m=
．
故答案为：
．
解：∵cosA=| 4 |
| 5 |
∴sinB=cosA=
| 4 |
| 5 |
∴cosB=
| 3 |
| 5 |
∵
| BD |
| BC |
∴BC=
| 5 |
| 3 |
∵AB=2m，
∴BC=
| 3 |
| 5 |
∴m=
| 25 |
| 7 |
故答案为：
| 25 |
| 7 |
点评：本题考查了解直角三角形，此题要能够根据等角的锐角三角函数建立要求的线段和已知的线段之间的关系．
练习册系列答案
相关题目
如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S2等于
如图，已知在Rt△ABC中，∠BAC=90°，AB=AC，M是AC的中点，AD⊥BM于E，交BC于D点．已知在Rt△ABC中，∠C=90°，sinA
，则tanB的值为（ ）
| ||
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
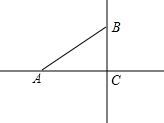如图：已知在Rt△ABC中，∠C=90°，AC=4，BC=3，在直线AC上找点P，使△ABP是等腰三角形，则AP的长度为