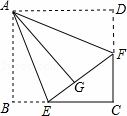
题目内容
如图,在平面直角坐标系中,O是坐标原点,直线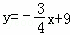 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线 经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
(1)求抛物线的解析式及点A的坐标;
(2)以OC为直径的⊙O′与BC交于点M,当t为何值时,PM与⊙O′相切?请说明理由.
(3)在点P从点A出发的同时,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒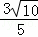 个单位长度的速度向点A运动,运动时间和点P相同.
个单位长度的速度向点A运动,运动时间和点P相同.
①记△BPQ的面积为S,当t为何值时,S最大,最大值是多少?
②是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.
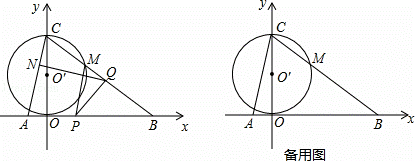
| 解:(1)在y=﹣ 中,令x=0,得y=9;令y=0,得x=12. ∴C(0,9),B(12,0). 又抛物线经过B,C两点,∴ ∴y=﹣ 于是令y=0,得﹣ 解得x1=﹣3,x2=12.∴A(﹣3,0). (2)当t=3秒时,PM与⊙O′相切.连接OM. ∵OC是⊙O′的直径,∴∠OMC=90°.∴∠OMB=90°. ∵O′O是⊙O′的半径,O′O⊥OP,∴OP是⊙O′的切线. 而PM是⊙O′的切线,∴PM=PO.∴∠POM=∠PMO. 又∵∠POM+∠OBM=90°,∠PMO+∠PMB=90°,∴∠PMB=∠OBM.∴PM=PB. ∴PO=PB= ∴当t=3秒,PM与⊙O′相切. (3)①过点Q作QD⊥OB于点D.
∵OC⊥OB,∴QD∥OC.∴△BQD∽△BCO.∴ 又∵OC=9,BQ=3t,BC=15,∴ ∴S△BPQ= S= ②存在△NCQ为直角三角形的情形. ∵BC=BA=15,∴∠BCA=∠BAC,即∠NCM=∠CAO. ∴△NCQ欲为直角三角形,∠NCQ≠90°,只存在∠NQC=90°和∠QNC=90°两种情况. 当∠NQC=90°时,∠NQC=∠COA=90°,∠NCQ=∠CAO, ∴△NCQ∽△CAO.∴ 当∠QNC=90°时,∠QNC=∠COA=90°,∠QCN=∠CAO, ∴△QCN∽△CAO.∴ 综上,存在△NCQ为直角三角形的情形,t的值为 |

 阅读快车系列答案
阅读快车系列答案下列计算正确的是( )
|
| A. |
| B. | (x+y)2=x2+y2 | C. | (﹣3x)3=﹣9x3 | D. | ﹣(x﹣6)=6﹣x |
如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为( )

|
| A. | 4 | B. | 3 | C. |
| D. | 2 |
 x+9
x+9 ,解得
,解得
 x2+
x2+ x+9.
x+9. x2+
x2+ OB=6.∴PA=OA+PO=3+6=9.此时t=3(秒).
OB=6.∴PA=OA+PO=3+6=9.此时t=3(秒).
 =
= .
. =
= ,解得QD=
,解得QD= t.
t. BP•QD=
BP•QD= .即S=
.即S= .
. .故当
.故当 时,S最大,最大值为
时,S最大,最大值为 .
. =
= .∴
.∴ =
= ,解得t=
,解得t= .
. =
= .∴
.∴ =
= ,解得
,解得 .
. 和
和 .
.
 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?