题目内容
 如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,
如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形,
(1)请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹);
(2)若∠AOB=30°,OE= ,求矩形AEBF的面积.
,求矩形AEBF的面积.
 解:作图如下:
解:作图如下:(1)连接AB,EF,交点设为P,
(2)∵∠AOB=30°,
∴AE=
 AO,
AO,∵OE=
 ,
,∴AE=2,AO=4,
∴BO=4,
∴EB=4-2
 ,
,∴矩形AEBF的面积为:2×(4-2
 )=8-4
)=8-4 .
.分析:(1)由条件OA=OB可联想到连接AB,得到等腰三角形OAB.根据等腰三角形的“三线合一”性质,要画出∠AOB的平分线,只需作底边AB上的中线,考虑到AB是矩形AEBF的对角线,根据矩形的性质,要作出AB的中点,只要连接EF,那么AB与EF的交点C就是AB的中点,从而过点C作射线OC就可得到∠AOB的平分线.
(2)首先利用勾股定理计算出AE、OB的长,进而得到EB的长,再求面积即可.
点评:此题主要考查了等腰三角形的性质以及矩形的性质和作复杂图形等知识,根据矩形性质作出图形是解决问题的关键.

练习册系列答案
相关题目
如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是( )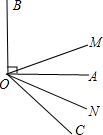

| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |


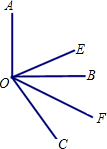 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC. 尺规作图:
尺规作图: 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).