题目内容
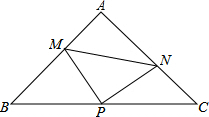 已知Rt△ABC中,∠A=90°,AB=AC.点P是BC的中点,M、N分别在AB、AC上.且PM⊥PN,连接MN.
已知Rt△ABC中,∠A=90°,AB=AC.点P是BC的中点,M、N分别在AB、AC上.且PM⊥PN,连接MN.(1)若M是AB中点,判断△PMN的形状并说明理由;
(2)若M是AB上任意一点,(1)的结论还成立么,为什么?
(3)当BM=4,CN=2时,求△PMN的面积和PM的长度.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)连接AP,可证AP=BP=CP,根据直角三角形斜边中线等于斜边一半性质即可求得PM=PB;
(2)连接AP,根据∠APC=∠EPF=90°,得出∠APE=90°-∠APF=∠BPF,再利用AP=BP,∠BAP=∠PBA=45°,即可得出△NAP≌△MBP,得出PN=PM;
(3)根据(2)中结论易证四边形AMPN面积=
△ABC面积,即可求得△PMN的面积,根据PM=PN即可解题.
(2)连接AP,根据∠APC=∠EPF=90°,得出∠APE=90°-∠APF=∠BPF,再利用AP=BP,∠BAP=∠PBA=45°,即可得出△NAP≌△MBP,得出PN=PM;
(3)根据(2)中结论易证四边形AMPN面积=
| 1 |
| 2 |
解答: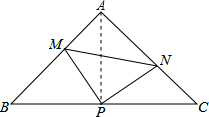 解:(1)连接AP,
解:(1)连接AP,
∵在△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴AP=BP=CP,
∵M是AB中点,
∴PM=
AB,PN=
AC,
∴PN=PM;
∴△PMN是等腰直角三角形;
(2)连接AP,则AP=PB=PC,
∵∠APC=∠APN+∠CPN=90°,∠MPN=∠MPA+∠APN=90°,
∴∠APM=∠CPN,
在△AMP和△CNP中,
,
∴△AMP≌△CNP(ASA),
∴MP=NP,
∴△PMN是等腰直角三角形;
(3)∵△AMP≌△CNP,
∴AM=CN,四边形AMPN面积=△ABP面积=
△ABC面积,
∵AB=BM+AM=BM+CN=6,
∴四边形AMPN面积=
×
(AB•AC)=9;
∵△AMN面积=
AM•AN=4,
∴△PMN的面积=9-4=5,
∵PM=PN,∠MPN=90°,
∴
PM•PN=5,
∴PM=PN=
.
 解:(1)连接AP,
解:(1)连接AP,∵在△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴AP=BP=CP,
∵M是AB中点,
∴PM=
| 1 |
| 2 |
| 1 |
| 2 |
∴PN=PM;
∴△PMN是等腰直角三角形;
(2)连接AP,则AP=PB=PC,
∵∠APC=∠APN+∠CPN=90°,∠MPN=∠MPA+∠APN=90°,
∴∠APM=∠CPN,
在△AMP和△CNP中,
|
∴△AMP≌△CNP(ASA),
∴MP=NP,
∴△PMN是等腰直角三角形;
(3)∵△AMP≌△CNP,
∴AM=CN,四边形AMPN面积=△ABP面积=
| 1 |
| 2 |
∵AB=BM+AM=BM+CN=6,
∴四边形AMPN面积=
| 1 |
| 2 |
| 1 |
| 2 |
∵△AMN面积=
| 1 |
| 2 |
∴△PMN的面积=9-4=5,
∵PM=PN,∠MPN=90°,
∴
| 1 |
| 2 |
∴PM=PN=
| 10 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AMP≌△CNP是解题的关键.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
二次函数y=2(x-4)2+5的开口方向、对称轴、顶点坐标分别是( )
| A、向下、直线x=-4、(-4,5) |
| B、向上、直线x=-4、(-4,5) |
| C、向上、直线x=4、(4,-5) |
| D、向上、直线x=4、(4,5) |
有一个人从甲地出发以7千米/时的速度到达乙地,又立即以9千米/时的速度返回甲地,则此人在往返过程中的平均速度为( )千米/时.
| A、8 | ||
B、
| ||
| C、7 | ||
D、
|
下列分式中,无论x取什么值,总是有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 南京市2014年的某10天中,每天的最低气温如图所示(单位:℃),则这10天中南京市最低气温的众数是
南京市2014年的某10天中,每天的最低气温如图所示(单位:℃),则这10天中南京市最低气温的众数是 如图,在直线AB上任意一点C,能用图中字母表示的射线共有
如图,在直线AB上任意一点C,能用图中字母表示的射线共有