题目内容
【题目】如图①，
、
两个圆柱形容器放置在同一水平桌面上，开始时容器中盛满水，容器中盛有高度为1 dm的水，容器下方装有一只水龙头，容器向容器匀速注水.设时间为t (s)，容器、中的水位高度
(dm)、
(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:
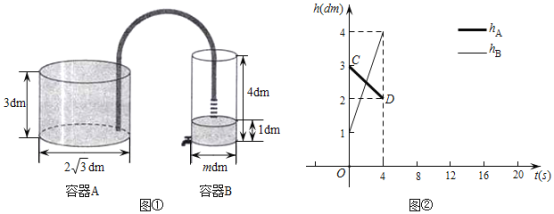
(1)容器向容器注水的速度为 dm3/s(结果保留
)，容器的底面直径
dm;
(2)当容器注满水后，容器停止向容器注水，同时开启容器的水龙头进行放水，放水速度为
dm3/s.请在图②中画出容器中水位高度与时间 (
)的函数图像，说明理由;
(3)当容器B注满水后，容器A继向容器B注水，同时开启容器B的水龙头进行放水，放水速度为
dm3/s，直至容器、水位高度相同时，立即停止放水和注水，求容器向容器全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)
【答案】（1）
，2；（2）见详解；（3）6s.
【解析】
（1）通过注水速度=注水体积÷注水时间以及圆柱体积=圆柱的底面积×圆柱的高，代入公式进行计算即可；
（2）通过放水时间=放水体积÷放水速度，求出时间即可求出放水时间，然后画出图像；
（3）列出容器A和容器B中水的高度与时间t的关系，通过水位高度相同求解即可．
解：（1）由图象可知，4秒时间A容器内水的高度下降了1dm，B容器内水的高度上升了3dm，B容器增加的水的体积等于A容器减少的水的体积，
A容器减少的水的体积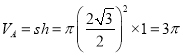
，
则注水速度为
，
B容器流入的水的体积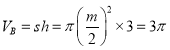
，
解得m=2，
故答案为；2．
（2）注满后B容器中水的总体积为：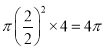
，
∵放水速度为
，
∴放空所需要的时间为：4π÷=16 s．
如图所示，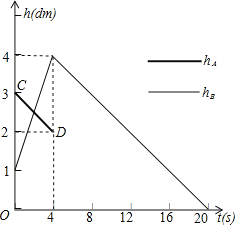
（3）4秒时A容器体积为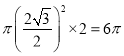
此时B容器体积为
根据注水速度，A容器内水的高度为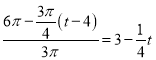
B容器内水的高度：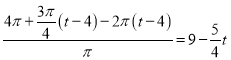
由
解得t=6，
∴容器A向容器B全程注水时间t为6s．
