Question

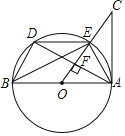
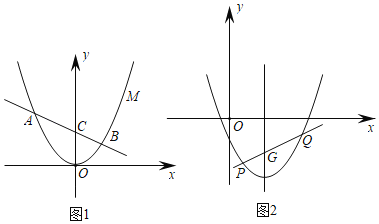
【题目】如图1，抛物线y＝ax2过定点M（，），与直线AB：y＝kx+1相交于A、B两点．

（1）若k＝﹣，求△ABO的面积．

（2）若k＝﹣，在抛物线上的点P，使得△ABP的面积是△ABO面积的两倍，求P点坐标．

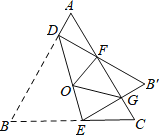
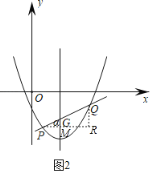
（3）将抛物线向右平移两个单位，再向下平移两个单位，得到抛物线C2，如题图2，直线y＝kx﹣2（k+）与抛物线C2的对称轴交点为G，与抛物线C2的交点为P、Q两点（点P在点Q的左侧），试探究是否为定值，并说明理由．

Answer 1

【答案】（1）；（2）点P（P′）的坐标为：（﹣1﹣，）或（﹣1，）；（3）为定值2，理由详见解析．

【解析】

（1）设点A、B的横坐标分别为：x1，x2，则，，即可求解；

（2）在直线AB上方作直线AB的平行线n交y轴于点N、交抛物线于点P（P′），过点O作直线AB的平行线l，根据三角形面积公式知，当CN＝2OC时，△ABP的面积是△ABO面积的两倍，即可求解；

（3）设点P、Q的横坐标分别为：x1，x2，则x1+x2＝4k+4，x1x2＝8k，同理x2﹣x1＝4，，则cosα＝，则PG＝＝，同理GQ＝，即可求解．

解：将点M的坐标代入抛物线表达式并解得：a＝，

故抛物线的表达式为：y＝x2…①；

（1）设点A、B的横坐标分别为：x1，x2，

k＝﹣，直线AB：y＝﹣x+1…②，

故点C（0，1），即OC＝1，

联立①②并整理得：x2+2x﹣4＝0，

故，，

，

△ABO的面积＝；

（2）在直线AB上方作直线AB的平行线n交y轴于点N、交抛物线于点P（P′），过点O作直线AB的平行线l，

根据三角形面积公式知，当CN＝2OC时，△ABP的面积是△ABO面积的两倍，

故点N（0，3），则直线n的表达式为：y＝﹣x+3…③，

联立①③并解得：x＝﹣1，

故点P（P′）的坐标为：（﹣1﹣，）或（﹣1，）；

（3）为定值，理由：

平移后抛物线的表达式为：y＝（x﹣2）2﹣2＝x2﹣x﹣1…④，

函数的对称轴为：x＝2，直线的表达式：y＝kx﹣2（k+）＝kx﹣2k﹣1…⑤，

则点G（2，﹣1），

设点P、Q的横坐标分别为：x1，x2，

联立④⑤并整理得：x2﹣4（k+1）x+8k＝0，

，，同理x2﹣x1＝4，

过点P作x轴的平行线交过点Q与y轴的平行线于点Q，交函数对称轴与点M，

由⑤知，tan∠QPRk＝tanα，则cosα，

则PG＝＝，同理GQ＝，

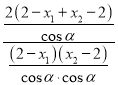
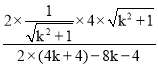
2为定值．