题目内容
已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于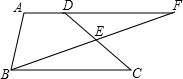 点F.
点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.
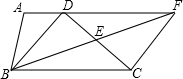 证明:(1)∵点E是DC中点∴DE=CE
证明:(1)∵点E是DC中点∴DE=CE又∵AD∥BC,F在AD延长线上,∴∠DFE=∠EBC,∠FDE=∠ECB
在△BCE与△FDE中
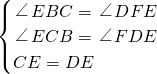 .
.∴△BCE≌△FDE(AAS)
(2)四边形BCFD是平行四边形.理由如下:
∵△BCE≌△FDE,
∴DE=CE,FE=BE.
∴四边形BCFD是平行四边形..
分析:(1)由平行线的性质可证,∠DFE=∠EBC,∠FDE=∠ECB,又已知DE=CE,在△BCE与△FDE中,根据三角形全等的判定定理,符合AAS的条件,即证△BCE≌△FDE.
(2)在1的基础上,可证DE=CE,FE=BE,根据平行四边形的判定,即证四边形BCFD是平行四边形.
点评:本题重点考查了三角形全等的判定定理,和平行四边形的判定,是一道较为简单的题目.

练习册系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )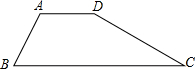 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=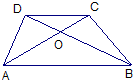 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.