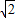Question

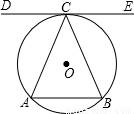
（2005•广州）如图，在直径为6的半圆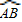上有两动点M、N，弦AM、BN相交于点P，则AP•AM+BP•BN的值为    ．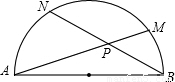

Answer 1

【答案】分析：连接AN、BM，根据圆周角定理，由AB是直径，可证∠AMB=90°，由勾股定理知，BP²=MP²+BM²，由相交弦定理知，AP•PM=BP•PN，原式=AP（AP+PM）+BP（BP+PN）=AP²+AP•PM+BP²+BP•PN=AP²+BP²+2AP•PM=AP²+MP²+BM²+2AP•PM=AP²+（AP+PM）²=AP²+AM²=AB²=36．
解答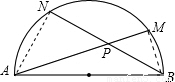：解：连接AN、BM，
∵AB是直径，
∴∠AMB=90°．
∴BP²=MP²+BM²
∵AP•PM=BP•PN
原式=AP（AP+PM）+BP（BP+PN）=AP²+AP•PM+BP²+BP•PN
=AP²+BP²+2AP•PM
=AP²+MP²+BM²+2AP•PM
=BM²+（AP+PM）²=BM²+AM²=AB²=36．
点评：本题利用了圆周角定理和相交弦定理，勾股定理求解．