题目内容
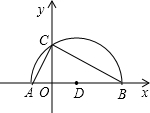
已知:如图,平面直角坐标系xOy中,A(1,0),B(0,1),C(-1,0),过点C的直线绕点C旋转,交y轴于点D,交线段AB于点E.
(1)求∠OAB的度数及直线AB的解析式;
(2)若△OCD与△BDE的面积相等,
①求直线CE的解析式;
②若y轴上的一点P满足∠APE=45°,请你直接写出P点的坐标.
解:(1)∵A(1,0),B(0,1),
∴OA=OB=1;
∵∠AOB=90°,
∴∠OAB=45°;
设直线AB的解析式为y=kx+b.
∴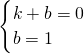 ,
,
解得,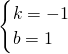 ,
,
∴直线AB的解析式为y=-x+1,
答:∠OAB的度数是45°,直线AB的解析式是y=-x+1.
(2)①∵S△COD=S△BDE,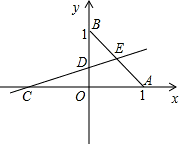
∴S△COD+S四边形AODE=S△BDE+S四边形AODE,
即S△ACE=S△AOB,
∵点E在线段AB上,
∴点E在第一象限,且yE>0,
∴ ×AC×yE=
×AC×yE= ×OA×OB,
×OA×OB,
∴ ×2×yE=
×2×yE= ×1×1,
×1×1,
yE= ,
,
把y= 代入直线AB的解析式得:
代入直线AB的解析式得: =-x+1,
=-x+1,
∴x= ,
,
设直线CE的解析式是:y=mx+n,
∵C(-1,0),E( ,
, )代入得:
)代入得: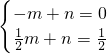 ,
,
解得:m= ,n=
,n= ,
,
∴直线CE的解析式为y= x+
x+ .
.
②P点的坐标为(0,0).
分析:(1)根据A、B的坐标和三角形的内角和定理求出∠OAB的度数即可;设直线AB的解析式为y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解即可;
(2)①推出三角形AOB和三角形ACE的面积相等,根据面积公式求出E的纵坐标,代入直线AB的解析式,求出E的横坐标,设直线CE的解析式是:y=mx+n,把E、C的坐标代入得出方程组,求出方程组的解即可;
②求出E再直线y=x上,根据等腰三角形的性质求出即可.
点评:本题考查了等腰三角形的性质,用待定系数法求一次函数的解析式,旋转的性质,三角形的面积等知识点,综合运用这些性质进行推理和计算是解此题的关键,此题题型较好,综合性比较强,但难度适中,通过做此题培养了学生分析问题和解决问题的能力.
∴OA=OB=1;
∵∠AOB=90°,
∴∠OAB=45°;
设直线AB的解析式为y=kx+b.
∴
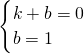 ,
,解得,
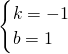 ,
,∴直线AB的解析式为y=-x+1,
答:∠OAB的度数是45°,直线AB的解析式是y=-x+1.
(2)①∵S△COD=S△BDE,

∴S△COD+S四边形AODE=S△BDE+S四边形AODE,
即S△ACE=S△AOB,
∵点E在线段AB上,
∴点E在第一象限,且yE>0,
∴
 ×AC×yE=
×AC×yE= ×OA×OB,
×OA×OB,∴
 ×2×yE=
×2×yE= ×1×1,
×1×1,yE=
 ,
,把y=
 代入直线AB的解析式得:
代入直线AB的解析式得: =-x+1,
=-x+1,∴x=
 ,
,设直线CE的解析式是:y=mx+n,
∵C(-1,0),E(
 ,
, )代入得:
)代入得: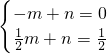 ,
,解得:m=
 ,n=
,n= ,
,∴直线CE的解析式为y=
 x+
x+ .
.②P点的坐标为(0,0).
分析:(1)根据A、B的坐标和三角形的内角和定理求出∠OAB的度数即可;设直线AB的解析式为y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解即可;
(2)①推出三角形AOB和三角形ACE的面积相等,根据面积公式求出E的纵坐标,代入直线AB的解析式,求出E的横坐标,设直线CE的解析式是:y=mx+n,把E、C的坐标代入得出方程组,求出方程组的解即可;
②求出E再直线y=x上,根据等腰三角形的性质求出即可.
点评:本题考查了等腰三角形的性质,用待定系数法求一次函数的解析式,旋转的性质,三角形的面积等知识点,综合运用这些性质进行推理和计算是解此题的关键,此题题型较好,综合性比较强,但难度适中,通过做此题培养了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
 BC=4
BC=4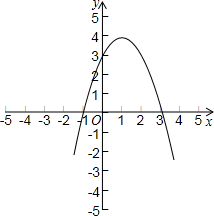 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.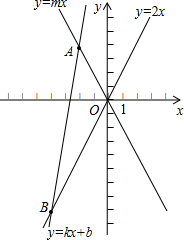 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).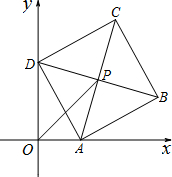 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.