题目内容
观察下列不等式,猜想规律并填空:12+22>2×1×2;(
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
(-2)2+32>2×(-2)×3;(
| 2 |
| 8 |
| 2 |
| 8 |
(-4)2+(-3)2>2×(-4)×(-3);(-
| 2 |
| 8 |
| 2 |
| 8 |
分析:根据已知的不等式发现:两个数的平方和大于两个数的积的2倍.所以a2+b2>2ab.
解答:解:规律为两个数的平方和大于两个数的积的2倍,所以a2+b2>2ab.
点评:此题只需观察已知的式子,即可发现规律.注意:此规律实际上是完全平方公式的运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 )2+(
)2+( )2>2×
)2>2× 2>2×
2>2×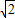 )2+(
)2+( )2>2×
)2>2×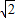 ×
×
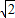 )2+
)2+ 2>2×
2>2× ×
×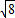 +
+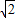 )2+(
)2+(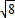 )2>2×
)2>2×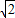 ×
× ,a2+b2> (a≠b).
,a2+b2> (a≠b).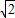 )2+(
)2+( )2>2×
)2>2×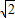 ×
×
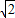 )2+
)2+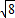 2>2×
2>2× ×
×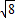 +
+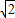 )2+(
)2+( )2>2×
)2>2×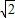 ×
×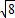 ,a2+b2> (a≠b).
,a2+b2> (a≠b).