Question

【题目】如图，在7×7网格中，每个小正方形的边长都为1．

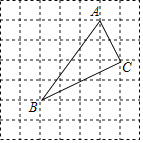
（1）建立适当的平面直角坐标系，使点A（3，4）、C（4，2），则点B的坐标为　 　；

（2）求图中格点△ABC的面积；

（3）判断格点△ABC的形状，并说明理由．

（4）在x轴上有一点P，使得PA+PC最小，则PA+PC的最小值是　 　．

Answer 1

【答案】（1）（0，0）；（2）5；（3）△ABC是直角三角形，理由见解析；（4）

【解析】

（1）首先根据A和C的坐标确定坐标轴的位置，然后确定B的坐标；

（2）利用矩形的面积减去三个直角三角形的面积求解；

（3）利用勾股定理的逆定理即可作出判断；

（4）作点C关于x轴的对称点C′连接AC′交x轴与点P，连接PC，依据轴对称图形的性质可得到PC＝PC′，然后依据两点之间线段最短可知当点A，P，C′在一条直线上时，AP+PC有最小值．

解：（1）B的坐标是（0，0）．

故答案是（0，0）；

（2）S△ABC＝4×4﹣×4×2﹣×3×4﹣×1×2＝5，

（3）∵AC2＝22+12＝5，BC2＝22+42＝20，AB2＝42+32＝25，

∴AC2+BC2＝AB2，

∴△ABC是直角三角形．

（4）如图1所示：作点C关于x轴的对称点C′连接AC′交x轴与点P，连接PC．

∵点C与点C′关于x轴对称，

∴PC＝PC′．

∴AP+PC＝AP+PC．

∴当A，P，C′在一条直线上时，AP+PC有最小值，最小值为AC′的长．

∵AC′＝＝．

∴AP+PC的最小值为．

故答案为：．