题目内容
如图，直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C，且相互平行，若L1、L2的距离为2，L2、L3的距离为4，则正方形的边长为分析：先作CF⊥L2，AE⊥L2，再利用全等三角形的判定和勾股定理求解．
解答：
解：如图，作CF⊥L2，垂足为F，AE⊥L2，垂足为E，
∴由同角的余角相等得，∠FCD=∠EDA，
又∵AD=CD，∠AED=∠CFD=90°，
∴△AED≌△DFC，
∴ED=CF=4，AE=2，
∴AD=
=2
．
解：如图，作CF⊥L2，垂足为F，AE⊥L2，垂足为E，∴由同角的余角相等得，∠FCD=∠EDA，
又∵AD=CD，∠AED=∠CFD=90°，
∴△AED≌△DFC，
∴ED=CF=4，AE=2，
∴AD=
| AE2+ED2 |
| 5 |
点评：本题利用了全等三角形的判定的性质，勾股定理，正方形的性质求解．
练习册系列答案
相关题目
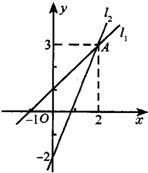-2），结合图象解答下列问题：
4、如图，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是（ ）
如图，直线l1与l2相交于点O，OM⊥l1，若∠α=44°，则∠β等于
如图，直线l1、l2、l3分别过正方形ABCD的三个顶点A，B，D，且相互平行，若l1与l2的距离为1，l2与l3的距离为1，则该正方形的面积是
如图，直线l1与l2相交于点P，l1的函数表达式y=kx+b，且经过（1，7）和（-3，-1）两点，点P的横坐标为-1，且l2交y轴于点A（0，-1）．