题目内容
 如图,将边长为
如图,将边长为 (n=1,2,3,…)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次是A1,A2,A3,…若摆放6个正方形纸片,则图中被遮盖的线段(虚线部分)之和为________.
(n=1,2,3,…)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次是A1,A2,A3,…若摆放6个正方形纸片,则图中被遮盖的线段(虚线部分)之和为________.
10
分析:过A1作A1A⊥EF于A,A1D⊥FG于D,根据正方形的性质推出∴∠A1AD=∠A1DC=∠EFG=90°,A1A=A1D,求出∠AA1B=∠DAAC,证△BAA1≌△CDA1,得到AB=DC,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可.
解答: 解:过A1作A1A⊥EF于A,A1D⊥FG于D,
解:过A1作A1A⊥EF于A,A1D⊥FG于D,
∵正方形EFGH,
∴∠A1AB=∠A1DC=∠EFG=90°,A1A=A1D,
∴∠AA1D=∠DA1C=90°,
∴∠AA1E=∠DAAC,
∴△DAA1≌△CDA1,
∴AB=DC,
∴BF+FC=FA+FD= =1,
=1,
同理第2个虚线之和是 =
= ,
,
同理第3个虚线之和是2,
同理第4个虚线之和是
同理第5个虚线之和是3,
∴1+ +2+
+2+ +3=
+3= ×(2+3+4+5+6)=10.
×(2+3+4+5+6)=10.
故答案为:10.
点评:本题主要考查对正方形的性质,全等三角形的判定等知识点的理解和掌握,能求出各个虚线的长度是解此题的关键.
分析:过A1作A1A⊥EF于A,A1D⊥FG于D,根据正方形的性质推出∴∠A1AD=∠A1DC=∠EFG=90°,A1A=A1D,求出∠AA1B=∠DAAC,证△BAA1≌△CDA1,得到AB=DC,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可.
解答:
 解:过A1作A1A⊥EF于A,A1D⊥FG于D,
解:过A1作A1A⊥EF于A,A1D⊥FG于D,∵正方形EFGH,
∴∠A1AB=∠A1DC=∠EFG=90°,A1A=A1D,
∴∠AA1D=∠DA1C=90°,
∴∠AA1E=∠DAAC,
∴△DAA1≌△CDA1,
∴AB=DC,
∴BF+FC=FA+FD=
 =1,
=1,同理第2个虚线之和是
 =
= ,
,同理第3个虚线之和是2,
同理第4个虚线之和是

同理第5个虚线之和是3,
∴1+
 +2+
+2+ +3=
+3= ×(2+3+4+5+6)=10.
×(2+3+4+5+6)=10.故答案为:10.
点评:本题主要考查对正方形的性质,全等三角形的判定等知识点的理解和掌握,能求出各个虚线的长度是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
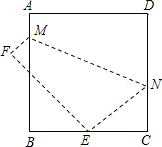 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )| A、3cm | B、4cm | C、5cm | D、6cm |
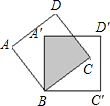 如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |

 如图,将边长为
如图,将边长为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为