题目内容
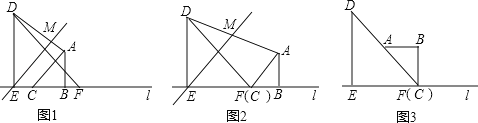
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .

【答案】(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,根据直线l:![]() 得:OM=
得:OM=![]() ,ON=3,由勾股定理得:MN=
,ON=3,由勾股定理得:MN=![]() =
=![]() ;
;
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,由cos∠ABD=cos∠ONM=![]() ,∴
,∴![]() ,AB=
,AB=![]() ,则AD=1,∵DG∥y轴,∴△MDG∽△MON,∴
,则AD=1,∵DG∥y轴,∴△MDG∽△MON,∴![]() ,∴
,∴![]() ,∴DG=
,∴DG=![]() ,∴CG=
,∴CG=![]() +
+![]() =
=![]() ,同理可得:
,同理可得:![]() ,∴
,∴![]() ,∴DH=
,∴DH=![]() ,∴C(
,∴C(![]() ,
,![]() );
);
②矩形在x轴上方时,同理可得:C(![]() ,
,![]() );
);
故答案为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目