题目内容
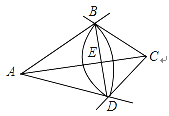
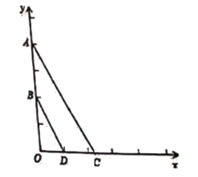
【题目】已知：如图，平面直角坐标系中，
，
，点C是x轴上一点，点D为OC的中点．
（1）求证：BD∥AC；
（2）若点C在x轴正半轴上，且BD与AC的距离等于2，求点C的坐标；
（3）如果
于点E，当四边形ABDE为平行四边形时，求直线AC的解析式．
【答案】（1）BD∥AC；（2）
；（3）
【解析】
（1）由A与B的坐标求出OA与OB的长，进而得到B为OA的中点，而D为OC的中点，利用中位线定理即可得证；
（2）如图1，作BF⊥AC于点F，取AB的中点G，确定出G坐标，由平行线间的距离相等求出BF的长，在直角三角形ABF中，利用斜边上的中线等于斜边的一半求出FG的长，进而确定出三角形BFG为等边三角形，即∠BAC=30°，设OC=x，则有AC=2x，利用勾股定理表示出OA，根据OA的长求出x的值，即可确定出C坐标；
（3）如图2，当四边形ABDE为平行四边形时，AB∥DE，进而得到DE垂直于OC，再由D为OC中点，得到OE=CE，再由OE垂直于AC，得到三角形AOC为等腰直角三角形，求出OC的长，确定出C坐标，设直线AC解析式为y=kx+b，将A与C坐标代入求出k与b的值，即可确定出AC解析式．
（1）
，
，
，
，点B为线段OA的中点，
点D为OC的中点，即BD为
的中位线，
；
（2）如图1，作
于点F，取AB的中点G，则
，
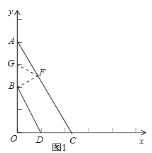
，BD与AC的距离等于2，
，
在
中，
，
，点G为AB的中点，
，
是等边三角形，
.
，
设
，则
，
根据勾股定理得：
，
，
，
点C在x轴的正半轴上，
点C的坐标为；
（3）如图2，当四边形ABDE为平行四边形时，
，
，
点D为OC的中点，
，
，
，
，
点C在x轴的正半轴上，
点C的坐标为
，
设直线AC的解析式为
.
将
，
得
，
解得：
.
直线AC的解析式为.
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
