题目内容
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
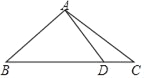
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

【答案】(1)①10;3;②![]() ;
;![]() ;③2;4;(2)当
;③2;4;(2)当![]() 或3时,
或3时,![]() ;(3)线段
;(3)线段![]() 的长度不变,是5.
的长度不变,是5.
【解析】
(1)根据题意即可得到结论;(2)由t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,于是得到![]() ,列方程即可得到结论;(3)由点M表示的数为
,列方程即可得到结论;(3)由点M表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,即可得到线段
,即可得到线段![]() 的长,线段
的长,线段![]() =5,即线段
=5,即线段![]() 的长度不变;
的长度不变;
解:
(1)①∵![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,
表示的数为8,
∴![]() ,AB的中点表示为
,AB的中点表示为![]() ;
;
故答案为:10,3;
②∵数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,
∴点![]() 表示的数为
表示的数为![]() ;
;
∵点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,
出发,以每秒2个单位长度的速度向左匀速运动,
∴点![]() 表示的数为
表示的数为![]() ;
;
故答案为:![]() ;
;![]() ;
;
③依题意得,![]() =
=![]() ,
,
∴t=2,
此时P、Q两点相遇,相遇点所表示的数为:-2+6=4;
故答案为:2,4;
(2)∵![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() ,
,
答:当![]() 或3时,
或3时,![]() ,
,
(3)点![]() 表示的数为
表示的数为![]() ,
,
点![]() 表示的数为
表示的数为![]() ,
,
∴![]() ,
,
∴线段![]() 的长度不变,是5.
的长度不变,是5.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】小洋八年级下学期的数学成绩(单位:分)如下表所示:
测试 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 测验4 | |||
成绩 | 106 | 102 | 115 | 109 | 112 | 110 |
(1)计算小洋该学期的数学平时平均成绩;
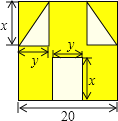
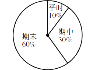
(2)如果该学期的总评成绩是根据如图所示的权重计算的,请计算出小洋该学期的数学总评成绩.
【题目】罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:
倍多15件,甲、乙两种商品的进价和售价如下表:![]() 注:获利
注:获利![]() 售价
售价![]() 进价
进价![]()
甲 | 乙 | |
进价 | 20 | 30 |
售价 | 29 | 40 |
![]() 罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
![]() 该购物中心第二次以第一次的进价又购进甲、乙两种商品
该购物中心第二次以第一次的进价又购进甲、乙两种商品![]() 其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?