题目内容
解下列方程:
(1)(2x-1)2=9
(2)x2+3x-4=0
(3)(x+4)2=5(x+4)
(4)x2+4x=2.
(1)(2x-1)2=9
(2)x2+3x-4=0
(3)(x+4)2=5(x+4)
(4)x2+4x=2.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法
专题:计算题
分析:(1)方程利用直接开平方法求出解即可;
(2)方程利用因式分解法求出解即可;
(3)方程移项后,利用因式分解法求出解即可;
(4)方程利用配方法求出解即可.
(2)方程利用因式分解法求出解即可;
(3)方程移项后,利用因式分解法求出解即可;
(4)方程利用配方法求出解即可.
解答:解:(1)方程开方得:2x-1=3或2x-1=-3,
解得:x1=2,x2=-1;
(2)分解因式得:(x-1)(x+4)=0,
解得:x1=1,x2=-4;
(3)方程变形得:(x+4)2-5(x+4)=0,
分解因式得:(x+4)(x+4-5)=0,
解得:x1=-4,x2=1;
(4)方程变形得:x2+4x+4=6,即(x+2)2=6,
开方得:x+2=±
,
解得:x1=-2+
,x2=-2-
.
解得:x1=2,x2=-1;
(2)分解因式得:(x-1)(x+4)=0,
解得:x1=1,x2=-4;
(3)方程变形得:(x+4)2-5(x+4)=0,
分解因式得:(x+4)(x+4-5)=0,
解得:x1=-4,x2=1;
(4)方程变形得:x2+4x+4=6,即(x+2)2=6,
开方得:x+2=±
| 6 |
解得:x1=-2+
| 6 |
| 6 |
点评:此题考查了解一元二次方程-因式分解法,配方法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
以2、4为两边长的三角形的第三边长是方程x2-7x+10=0的根,则这个三角形的周长为( )
| A、8 | B、11 |
| C、11或8 | D、以上都不对 |
 如图,?ABCD的对角线相交于点O,AB=8cm,两条对角线长的和为24cm,则△COD的周长为( )
如图,?ABCD的对角线相交于点O,AB=8cm,两条对角线长的和为24cm,则△COD的周长为( )| A、32cm | B、24cm |
| C、20cm | D、16cm |
下面说法正确的是( )
| A、0不是自然数 |
| B、0是最小的有理数 |
| C、0是最小的整数 |
| D、0是绝对值最小的有理数 |
 如图,反比例函数y=
如图,反比例函数y=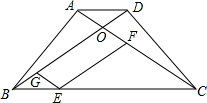 (1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
(1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.