题目内容
 在△ABC中,∠BAC=90°,延长BA到D,使AD=
在△ABC中,∠BAC=90°,延长BA到D,使AD= AB,点E、F分别为边BC、AC的中点.
AB,点E、F分别为边BC、AC的中点.
(1)求证:DF=BE;
(2)若CF=2,CE= .求tan∠ADF.
.求tan∠ADF.
(1)证明:∵F,E是AC,BC的中点,
∴FE= AB(中位线定理);
AB(中位线定理);
∵AD= AB,
AB,
∴AD=FE,
∵点F是AC中点,
∴AF=FC,
又∠DAF=∠CFE=90°,
∴△DAF≌△FEC,
∴DF=EC,
∴DF=BE;
(2)解:∵CF=2,CE= ,
,
∴EF=1,
∴tan∠ADF=tan∠CEF=2.
分析:(1)连接GF,易得AF是GD的中垂线,所以AD=AG.又∠BAC=90°,即AF⊥BD,所以DF=FG.因为EF为△ABC的中位线,所以BG=EF,BG∥EF,所以四边形BEFG为平行四边形,所以GF=BE.
(2)将∠ADF的正弦值转化为∠CEF的正弦值求即可.
点评:本题考查了三角形的中位线定理及锐角三角函数的定义.用了中垂线的判定和性质,三角形中位线的性质,平行四边形的判定和性质求解.
∴FE=
 AB(中位线定理);
AB(中位线定理);∵AD=
 AB,
AB,∴AD=FE,
∵点F是AC中点,
∴AF=FC,
又∠DAF=∠CFE=90°,
∴△DAF≌△FEC,
∴DF=EC,
∴DF=BE;
(2)解:∵CF=2,CE=
 ,
,∴EF=1,
∴tan∠ADF=tan∠CEF=2.
分析:(1)连接GF,易得AF是GD的中垂线,所以AD=AG.又∠BAC=90°,即AF⊥BD,所以DF=FG.因为EF为△ABC的中位线,所以BG=EF,BG∥EF,所以四边形BEFG为平行四边形,所以GF=BE.
(2)将∠ADF的正弦值转化为∠CEF的正弦值求即可.
点评:本题考查了三角形的中位线定理及锐角三角函数的定义.用了中垂线的判定和性质,三角形中位线的性质,平行四边形的判定和性质求解.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.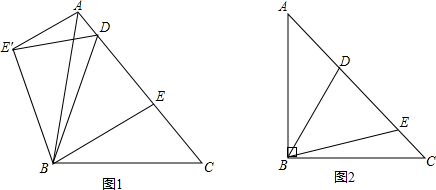
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.