题目内容
有一群猴子，一天结伴去偷桃子．分桃子时，如果每只猴子分3个，那么还剩下59个；如果每只猴子分5个，就都分得桃子，但有一只猴子分得的桃子不够5个．你能求出有几只猴子，几个桃子吗？
解：设有
只猴子，则有
个桃子，
根据题意，得
，解得
.
因为为整数，所以
或
当时，
当
时，
答：有
只猴子，
个桃子；或有
只猴子，
个桃子．
名题金卷系列答案
于点
，
于点
，
．请问：
平分
吗？若平分，请说明理由．
的不等式组
的解集为
，则
的值分别为___________.
；如图,已知平面内有两条直线AB、CD,且
AB∥CD,P为一动点.
 |
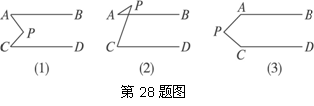(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到AB的外侧时,如图(2),是否仍有(1)的结论?如果不是__
______________,请写出你的猜想(不要求证明).
(3)当点P移动到如图(3)的位置时,∠P与∠A、∠C又有怎样的关系?能否利用(1)的结论来证明?还有其他的方法吗?请写出一种.
某市民政部门：五一期间举行“即开式福利彩票”的销售活动，发行彩票10万张（每张彩票2元），在这些彩票中，设置如下奖项：
| 奖金（元） | 1 000 | 500 | 100 | 50 | 10 | 2 |
| 数量（个） | 10 | 40 | 150 | 400 | 1 000 | 10 000 |
如果花2元钱购买1张彩票，那么所得奖金不少于50元的概率是（ ）
A.
B.
C.
D.
小颖和小红两名同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：
| 朝上的点 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
数
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投
掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
是第二象限的点，则
的取值范围是 .