题目内容
2.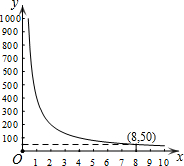 码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.
码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.(1)求y与x之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
分析 【分析】(1)根据题意即可知装载速度y(吨/天)与装完货物所需时间x(天)之间是反比例函数关系,则可求得答案;
(2)由x=5,代入函数解析式即可求得y的值,即求得平均每天至少要卸的货物;
(3)由10名工人,每天一共可卸货50吨,即可得出平均每人卸货的吨数,即可求得答案.
解答 解:(1)设y与x之间的函数表达式为y=$\frac{k}{x}$,
根据题意得:50=$\frac{k}{8}$,
解得k=400,
∴y与x之间的函数表达式为y=$\frac{400}{x}$;
(2)∵x=5,∴y=80,
解得:y=80;
答:平均每天至少要卸80吨货物;
(3)∵每人一天可卸货:50÷10=5(吨),
∴80÷5=16(人),16-10=6(人).
答:码头至少需要再增加6名工人才能按时完成任务.
点评 此题考查了反比例函数的应用.解题的关键是理解题意,根据题意求函数的解析式.

练习册系列答案
相关题目
13.计算(-3)2003÷(-3)2005的结果为( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9\;}$ | D. | $-\frac{1}{9\;}$ |
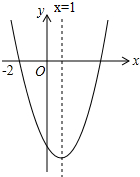 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.
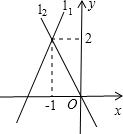 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.