题目内容
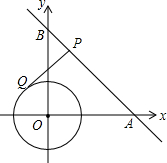 如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )A、
| ||
| B、3 | ||
C、3
| ||
D、
|
考点:切线长定理
专题:
分析:连接OP.根据勾股定理知PQ2=OP2-OQ2,当OP⊥AB时,线段OP最短,即线段PQ最短.
解答: 解:连接OP、OQ.
解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=6
∴OP=
AB=3
,
∵OQ=2,
∴PQ=
=
,
故选:D.
 解:连接OP、OQ.
解:连接OP、OQ.∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=6
| 2 |
∴OP=
| 1 |
| 2 |
| 2 |
∵OQ=2,
∴PQ=
| OP2-QO2 |
| 14 |
故选:D.
点评:本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角来解决有关问题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
在代数式
,3-x,2x2y,
,0,
a中,单项式有( )
| m+n |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| A、4个 | B、3个 | C、2个 | D、1个 |
单项式
的系数和次数分别是( )
| 4πxy3 |
| 5 |
A、
| ||
B、
| ||
| C、4π,4 | ||
D、
|
在-4,0.3,
这四个数中,是无理数的是( )
| 2 |
| A、-4 | ||
| B、0.3 | ||
C、
| ||
D、
|
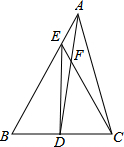 如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证:
如图,在△ABC中,D为BC的中点,AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,求证: