题目内容
已知:如图,直线y=kx+b与x轴、y轴分别交于点A、B两点,OA=OB=1,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,射线PQ交x轴于点Q.
(1)求直线AB的解析式.
(2)△OPQ能否是等腰三角形?如果能,请求出点P的坐标;若不能,请说明理由.
(3)无论m为何值,(2)中求出的P点是否始终在直线y=mx+
(m≠0)上?请说明理由.

(1)求直线AB的解析式.
(2)△OPQ能否是等腰三角形?如果能,请求出点P的坐标;若不能,请说明理由.
(3)无论m为何值,(2)中求出的P点是否始终在直线y=mx+
| 1-m |
| 2 |

(1)由OA=OB=1可知点A、B的坐标是A(0,1),B(1,0),
把A(0,1),B(1,0)代入y=kx+b得:
,
解得:k=-1,b=1,
则y=-x+1;
(2)△OPQ可以是等腰三角形.
过P点PE⊥OA交OA于点E,
(ⅰ)若OP=OQ,
则∠OPQ=∠OQP=∠OPQ,
∴∠POQ=90°,
∴点P与点A重合,
∴点P坐标为(0,1),
(ⅱ)若QP=QO,
则∠OPQ=∠QOP=45°,
所以PQ⊥QO,
可设P(x,x)代入y=-x+1得x=
,
∴点P坐标为(
,
),
(ⅲ)若PO=PQ,
∵∠OPQ+∠1=∠2+∠3,
而∠OPQ=∠3=45°,
∴∠1=∠2,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
PB=OA=1,
∴AP=
-1
由勾股定理求得PE=AE=1-
,
∴EO=
,
∴点P坐标为(1-
,
),
∴点P坐标为(0,1)或(
,
)或(1-
,
)时,△OPQ是等腰三角形.
(3)把x=0代入y=mx+
≠1;
把x=
代入y=mx+
=
;
把x=1-
代入y=mx+
≠
,
所以,(2)中求得的点P,只有当点P坐标为(
,
)时,P点始终在直线y=mx+
(m≠0)上.

把A(0,1),B(1,0)代入y=kx+b得:
|
解得:k=-1,b=1,
则y=-x+1;
(2)△OPQ可以是等腰三角形.
过P点PE⊥OA交OA于点E,
(ⅰ)若OP=OQ,
则∠OPQ=∠OQP=∠OPQ,
∴∠POQ=90°,
∴点P与点A重合,
∴点P坐标为(0,1),
(ⅱ)若QP=QO,
则∠OPQ=∠QOP=45°,
所以PQ⊥QO,
可设P(x,x)代入y=-x+1得x=
| 1 |
| 2 |
∴点P坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
(ⅲ)若PO=PQ,
∵∠OPQ+∠1=∠2+∠3,
而∠OPQ=∠3=45°,
∴∠1=∠2,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
PB=OA=1,
∴AP=
| 2 |
由勾股定理求得PE=AE=1-
| ||
| 2 |
∴EO=
| ||
| 2 |
∴点P坐标为(1-
| ||
| 2 |
| ||
| 2 |
∴点P坐标为(0,1)或(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(3)把x=0代入y=mx+
| 1-m |
| 2 |
把x=
| 1 |
| 2 |
| 1-m |
| 2 |
| 1 |
| 2 |
把x=1-
| ||
| 2 |
| 1-m |
| 2 |
| ||
| 2 |
所以,(2)中求得的点P,只有当点P坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
| 1-m |
| 2 |


练习册系列答案
相关题目

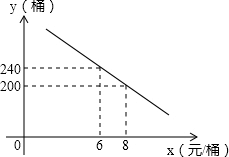 费用是a元.
费用是a元.

