题目内容
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
(3)在(2)的条件下,求弧BD的长.
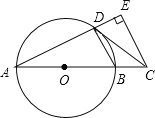
【答案】(1)证明见解析;(2)4![]() (3)
(3)![]()
【解析】
试题![]() 连接
连接![]() ,由
,由![]() 是
是![]() 切线,得到
切线,得到![]() ,根据
,根据![]() 为
为![]() 的直径,得到
的直径,得到![]() 等量代换得到
等量代换得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() 即可得到结论;
即可得到结论;![]() 根据垂直的定义得到
根据垂直的定义得到![]() 根据平行线的性质得到
根据平行线的性质得到![]() 根据相似三角形的性质得到
根据相似三角形的性质得到![]() 解方程即可得到结论;
解方程即可得到结论;
![]() 利用三角函数求得
利用三角函数求得![]() 的度数,则
的度数,则![]() 即可求得,然后在直角
即可求得,然后在直角![]() 中求得
中求得![]() ,从而求得半径,然后利用弧长公式求解.
,从而求得半径,然后利用弧长公式求解.
试题解析:![]() 证明:连接
证明:连接![]() ,
,
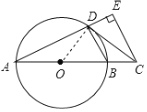
∵![]() 是
是![]() 切线,
切线,
∴![]() ,
,
即![]()
∵![]() 为
为![]() 的直径,
的直径,
![]()
即![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 在直角
在直角![]() 中,
中,![]()
![]()
![]()
![]()
![]() 是等边三角形,则
是等边三角形,则![]()
则![]() 的长是
的长是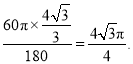

练习册系列答案
相关题目