Question

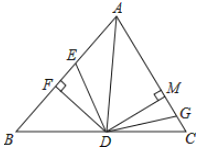
【题目】在△ABC中，AB=AC，点D在边AC上，连接BD，点E在边AB上，△BCD和△BED关于BD对称，若△ADE是等腰三角形，则( )

A.B.C.D.

Answer 1

【答案】A

【解析】

根据轴对称关系及AB=AC得到∠ABC=∠C=∠BED，设∠BAC=x，再根据△ADE是等腰三角形，分三种情况计算得出x的值.

∵△BCD和△BED关于BD对称，

∴∠BED=∠C,

∵AB=AC,

∴∠ABC=∠C=∠BED,

设∠BAC=x

△ADE是等腰三角形，

当AE=DE时，∠BED=2x，可得2x+2x+x=180，得x=；

当AE=AD时，∠BED=180-(180-x)= 90+x，可得2（90+x）+x=180，无解；

当AD=DE时，∠BED=180-x，可得2（180-x）+x=180，得x=180，舍去，

故选：A.