题目内容
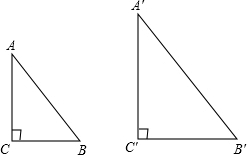
如果Rt△ABC∽Rt△A′B′C′,∠C=∠C'=90°,AB=3,BC=2,A′B′=12,求A′C′的长.
分析:利用勾股定理列式求出AC,然后根据相似三角形对应边成比例列式计算即可得解.
解答:解:在Rt△ABC中,∵∠C=90°,AB=3,BC=2,
∴AC=
=
,
∵Rt△ABC∽Rt△A′B′C′,
∴
=
,
即
=
,
解得A′C′=4
.
∴AC=
| 32-22 |
| 5 |
∵Rt△ABC∽Rt△A′B′C′,
∴
| AB |
| A′B′ |
| AC |
| A′C′ |
即
| 3 |
| 12 |
| ||
| A′C′ |
解得A′C′=4
| 5 |
点评:本题考查了相似三角形对应边成比例的性质,勾股定理的应用,熟记性质是解题的关键.

练习册系列答案
相关题目