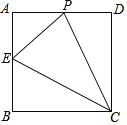
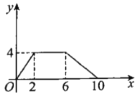
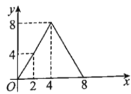
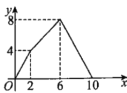
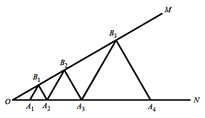
��Ŀ����
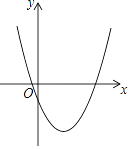
����Ŀ��������C1��y1=mx2��4mx+2n��1��ƽ����x���ֱ�߽���A��B���㣬��A������Ϊ����1��2��������ͼ��������½��ۣ��ٶԳ���Ϊֱ��x=2������������y�ύ������Ϊ��0����1������m��![]() ������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��
������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��![]() ��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��
��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��
A. 2�� B. 3�� C. 4�� D. 5��
���𰸡�B
��������
���������ߵĶԳ���ֱ�߹�ʽ��������öԳ���ֱ�ߣ�������������������Ľ���������ص㣬�ó�C�������Ϊ����0��2n-1��;��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m,�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��������б�ʽӦ�ô���0���Ӷ��г�����m�IJ���ʽ�����m��ȡֵ��Χ���������ߵĶԳ��ԣ�B�������ΪB��5��2������![]() ��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ
��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ![]() ,�Ӷ��ó�a��ȡֵ��Χ������ʽ
,�Ӷ��ó�a��ȡֵ��Χ������ʽ![]() �Ľ���Կ����ǣ�������
�Ľ���Կ����ǣ�������![]() λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������
λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������![]() ����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
�������ߵĶԳ���Ϊֱ��![]() ��������ȷ��
��������ȷ��
�ڵ�x=0ʱ��y=2n-1,�ʢڴ���
�� ��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m
�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��
![]() ��������:
��������:![]()
��ã�m>![]() ����������.
����������.
���������ߵĶԳ��ԣ�B�������ΪB��5��2��
�����߶ηֱ�����ֻ��һ��������
��ʱ��a��ֵ�ֱ�Ϊ![]()
�ó�a��ȡֵ��Χ,��![]() ���ʢ���ȷ.
���ʢ���ȷ.
�ݲ���ʽ![]() �Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.
�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д�����Ŀ��Ϊ�������ǽ�Լ��ˮ����ʱ��©ˮ��ˮ��ͷ��С��ͬѧ����ˮ��ͷ©ˮʵ�飬ÿ��10��۲���Ͳ��ˮ���������¼�����������©����ˮ����ȷ��1����������֪���ڽ�ˮ����Ͳ�������Ϊ100������
ʱ��t���룩 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
��Ͳ��ˮ��v�������� | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
��1����ͼ�е�ƽ��ֱ������ϵ�У��ԣ�t,v��Ϊ��������ϱ������ݶ�Ӧ�ĵ㣻
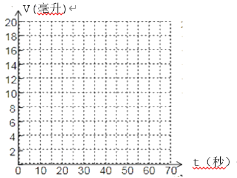
��2���ù⻬���������Ӹ��㣬��²�V��t�ĺ�����ϵʽ��______________��
��3��������⣺
��С��ͬѧ������Ͳ��ʼʵ��ǰԭ�д�ˮ ������
�����С��ͬѧ����ʵ�飬����Ͳ�е�ˮ�պ�ʢ��ʱ������ʱ����_____����
������©ˮ�ٶȣ���Сʱ��©ˮ ������
����Ŀ��ijУҪ������ѧ�����������س������¡��ź�����ѡһ�˲μ�У����Զ����������Զר������Լ��Ժ��![]() ����Զѡ�����У����ǵijɼ�����λ��
����Զѡ�����У����ǵijɼ�����λ��![]() �����±���ʾ��
�����±���ʾ��
ר����Ժ� | ƽ���� | ���� | |||||||
���� |
|
|
|
|
|
|
|
| |
�ź� |
|
|
|
|
|
|
|
| |
![]() ���ź�ͬѧ
���ź�ͬѧ![]() �β��Գɼ���ƽ����������ͬѧ
�β��Գɼ���ƽ����������ͬѧ![]() �β��Գɼ��ķ��
�β��Գɼ��ķ��
![]() ����ֱ��ƽ�����ͷ���ĽǶȷ������˳ɼ����ص㣻
����ֱ��ƽ�����ͷ���ĽǶȷ������˳ɼ����ص㣻
![]() ������������������ϣ��ɼ����ﵽ
������������������ϣ��ɼ����ﵽ![]() ���ͺܿ��ܵõ��ھ�������ΪӦѡ˭ȥ������ھ��Ƚ��а��գ�˵�����ɣ�
���ͺܿ��ܵõ��ھ�������ΪӦѡ˭ȥ������ھ��Ƚ��а��գ�˵�����ɣ�
![]() �����ĸ�����óɼ��ļ�¼��
�����ĸ�����óɼ��ļ�¼��![]() ����Ҫ����Ƽ�¼������ΪӦѡ˭ȥ������
����Ҫ����Ƽ�¼������ΪӦѡ˭ȥ������