题目内容
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠BAC＝30º，EF⊥AB，垂足为F，连结DF．
（1）求证：AC＝EF；
（2）求证：四边形ADFE是平行四边形．
（1）∵在等边△ABE中，EF⊥AB，
∴AF= 
AE= AB,
又∵Rt△ABC，∠BAC＝30º，
∴BC=AB,
∴BC=AF
∴Rt△ABC∽Rt△EAF（AAS）
即AC=EF
（2）因为EF⊥AB，∴，∠AFE=90
∵△ACD是等边三角形，∴∠DAC=60，∴∠DAB=90
∵∠AFE=∠DAB，∴AD//EF
∵∠BAC=30，∴CB=AB
∵EF⊥AB，∴AF=AB=CB
∵AF=CB.AD=AC,∠DAB=∠ACB=90
∴Rt△ABC∽Rt△DFA
∴∠ADF=∠CAB=30，
∵∠DAB+∠BAE=90+60=150
∴∠ADF+∠DAE=180
∴AE//DF
∴四边形ADFE是平行四边形
解析
练习册系列答案
华东师大版一课一练系列答案
相关题目
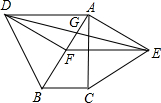如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC=30°，下列结论：①EF⊥AC；②四边形ADFE为平行四边形；③AD=4AG；④△DBF≌△EFA．其中正确结论的序号是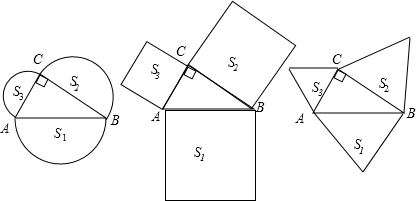
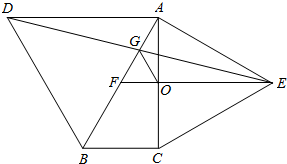如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，连接DF、EF、DE，EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：
如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB中点，连接DF、EF，DE、EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．其中正确的结论的序号是
如图，分别以Rt△ABC三边为边向外作三个正方形，其面积分别用S1、S2、S3表示，容易得出S1、S2、S3之间有的关系式