题目内容
 如图,已知直线AB、CD相交于O,OE⊥AB,垂足为O,OF平分∠AOC,∠AOF:∠AOD=5:26,求∠EOC.
如图,已知直线AB、CD相交于O,OE⊥AB,垂足为O,OF平分∠AOC,∠AOF:∠AOD=5:26,求∠EOC.
解:∵OF平分∠AOC,
∴∠AOF=∠COF,
∵∠AOF:∠AOD=5:26,
∴设∠AOF=5x,则∠AOD=26x,∠FOC=5x,
∴5x+5x+26x=36x=180°,
解得:x=5°,
∴∠AOF=∠COF=25°,
∴∠EOC=∠EOA+∠AOC=90°+50°=140°.
分析:首先根据角平分线的性质得出∠AOF=∠COF,进而得出∠AOF=∠COF=25°,即可得出答案.
点评:此题主要考查了垂线的定义以及平角的定义和角平分线的性质等知识,根据已知得出∠AOF=∠COF的度数是解题关键.
∴∠AOF=∠COF,
∵∠AOF:∠AOD=5:26,
∴设∠AOF=5x,则∠AOD=26x,∠FOC=5x,
∴5x+5x+26x=36x=180°,
解得:x=5°,
∴∠AOF=∠COF=25°,
∴∠EOC=∠EOA+∠AOC=90°+50°=140°.
分析:首先根据角平分线的性质得出∠AOF=∠COF,进而得出∠AOF=∠COF=25°,即可得出答案.
点评:此题主要考查了垂线的定义以及平角的定义和角平分线的性质等知识,根据已知得出∠AOF=∠COF的度数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于
13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于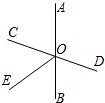 15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=
15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=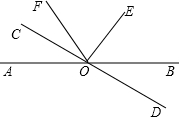 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数. 如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF. 如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.
如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.