题目内容

已知线段a，b，c组成了一个三角形．求证： $数学公式$ ， $数学公式$ ， $数学公式$ 也能组成一个三角形．

证明：由已知设|b-c|＜a＜b+c，
由a＜b+c，得（ $\text{[math]}$ ）²＜b+c＜（ $\text{[math]}$ ）²，
∴ $\text{[math]}$ ＜ $\text{[math]}$ + $\text{[math]}$ ；
又∵| $\text{[math]}$ - $\text{[math]}$ |（ $\text{[math]}$ + $\text{[math]}$ ）=|b-c|＜a=（ $\text{[math]}$ ）²，
∴| $\text{[math]}$ - $\text{[math]}$ |＜ $\text{[math]}$ ＜ $\text{[math]}$ = $\text{[math]}$ ，
∴| $\text{[math]}$ - $\text{[math]}$ |＜ $\text{[math]}$ ；
综上，得| $\text{[math]}$ - $\text{[math]}$ |＜ $\text{[math]}$ ＜ $\text{[math]}$ + $\text{[math]}$ ，
同理可得：| $\text{[math]}$ - $\text{[math]}$ |＜ $\text{[math]}$ ＜ $\text{[math]}$ + $\text{[math]}$ ，
| $\text{[math]}$ - $\text{[math]}$ |＜ $\text{[math]}$ ＜ $\text{[math]}$ + $\text{[math]}$ ；
∴ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 也能组成一个三角形．
分析：构成三角形的三边必须满足：任意一边大于另外两边之差，而小于两边之和，已知线段a，b，c组成了一个三角形，故有|b-c|＜a＜b+c等，围绕这个不等式组进行平方、开平方运算即可．只证三种情况中的一种，其它同理可证．
点评：本题考查了二次根式中判断三角形三边关系中的运用．关键是由已知不等式构造新的不等式，运用平方或开平方的方法进行证题．

练习册系列答案

相关题目

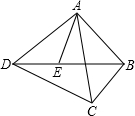如图，点E是四边形ABCD的对角线BD上的一点，且∠BAC=∠BDC=∠DAE．
（1）试说明：BE•AD=CD•AE；
（2）根据图形的特点，猜想

可能等于哪两条线段的比？并说明你的猜想是正确的．（注：只需写出图中已知线段的一组比即可）

作图与回答：
（1）如图1，已知线段a和b，请用直尺和圆规作出线段AB，使AB=2a-b．（不必写作法，只需保留作图痕迹）
（2）已知直线AB与CD垂直，垂足为O，请在图中用量角器画射线OE表示北偏西30°、画射线OF表示南偏东30°、画射线OH表示北偏东45°．
（3）找一找，你完成的作如图2中是锐角的对顶角有几组，把它们写出来．

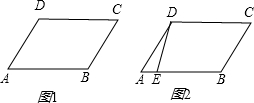已知，如图1：四边形ABCD中，AB=CD，AD=BC，试回答下列问题：
（1）说明：∠A=∠C；
（2）如图2若E、F分别在AB、CD上且AE=CF，请你以F为一个端点，和图中已标明字母的某点连接成一条新段，猜想并说明它与图中哪条已知线段相等（只需说明一组）
①我连接

，并猜想

．
②理由：
（3）若E、F分别在AB、CD上且DE=BF，此时AE=CF成立吗？若成立，说明理由，若不成立，也说明理由或画出示意图．

作图与回答：
（1）已知线段a和b, 请用直尺和圆规作出线段AB，使AB＝2a―b.（不必写作法，只需保留作图痕迹）

（2）已知直线AB与CD垂直，垂足为O，请在图中用量角器画射线OE表示北偏西30°、画射线OF表示南偏东30°、画射线OH表示北偏东45°.

（3）找一找，你完成的作图（2）中是锐角的对顶角有几组，
把它们写出来.

作图与回答：

（1）已知线段a和b, 请用直尺和圆规作出线段AB，使AB＝2a―b.（不必写作法，只需保留作图痕迹）

（2）已知直线AB与CD垂直，垂足为O，请在图中用量角器画射线OE表示北偏西30°、画射线OF表示南偏东30°、画射线OH表示北偏东45°.

（3）找一找，你完成的作图（2）中是锐角的对顶角有几组，

把它们写出来.

已知线段a，b，c组成了一个三角形．求证：，，也能组成一个三角形．

试题分类

已知线段a，b，c组成了一个三角形．求证： $数学公式$ ， $数学公式$ ， $数学公式$ 也能组成一个三角形．