题目内容
一元二次方程x2+mx+1=0有实数根,不等式组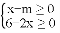 有解,则m应满足的条件是( )
有解,则m应满足的条件是( )
A. m≥2 B. m≤﹣2
C. m≤﹣2或2≤m≤3 D. 2≤m<3
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
题目内容
一元二次方程x2+mx+1=0有实数根,不等式组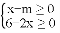 有解,则m应满足的条件是( )
有解,则m应满足的条件是( )
A. m≥2 B. m≤﹣2
C. m≤﹣2或2≤m≤3 D. 2≤m<3
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案