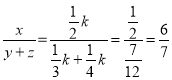Question

【题目】在“我为武汉加油”征文活动中，学校计划对获得一、二等奖的学生分别奖励一台计算器，一个考试包．已知购买台计算器和个考试包共元，购买台计算器和个考试包共元．

（1）计算器、考试包的单价分别为多少元？

（2）经与商家协商，购买计算器超过台时，每增加一台，单价降低元；超过台，均按购买台的单价销售，考试包一律按原价销售，学校计划奖励一、等奖学生共计人，其中一等奖的人数不少于人，且不超过人，这次奖励一等奖学生多少人时，购买奖品金额最少，最少为多少元？

Answer 1

【答案】（1）计算器、考试包的单价分别为元、元；（2）当一等奖人数为时花费最少，最少为元．

【解析】

根据题意列出二元一次方程组解出即可;

由题意列出总金额与单价和数量的函数关系,再分别讨论30-50及50-60的金额进行对比．

解：（1）设计算器、考试包的单价分别为元、元．

根据题意可得,

解得

答：计算器、考试包的单价分别为元、元．

（2）设计算器单价为元,购买数量为台,支付计算器和考试包总金额为元．

①当时,．

．

当时,,当时,,

当时,．

②当时,,,,

当时,的最小值为元．

当一等奖人数为时花费最少,最少为元．