题目内容
(本题满分10分)如图,在 中,
中, ,
, ,
, .点
.点 、
、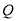 都是斜边
都是斜边 上的动点,点
上的动点,点 从
从 向
向 运动(不与点
运动(不与点 重合),点
重合),点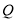 从
从 向
向 运动,
运动, .点
.点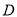 、
、 分别是点
分别是点 、
、 以
以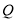 、
、 为对称中心的对称点,
为对称中心的对称点, 于
于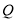 ,交
,交 于点
于点 .当点
.当点 到达顶点
到达顶点 时,
时, 、
、 同时停止运动.设
同时停止运动.设 的长为
的长为 ,
, 的面积为
的面积为 .
.

(1)求证: ∽
∽ ;
;
(2)求 关于
关于 的函数解析式;
的函数解析式;
(3)当 为何值时,
为何值时, 为等腰三角形?
为等腰三角形?
(1)证明有两组角对应相等,过程略;(2) ;
;
(3) 或
或 或
或 或
或
【解析】
试题分析:(1)由点对称可得 ,再加上
,再加上 和
和 ,即可利用两组角对应相等得到两个三角形相似;(2)要求
,即可利用两组角对应相等得到两个三角形相似;(2)要求 的面积,需求得
的面积,需求得 和
和 ,根据相似三角形的相似比,可得
,根据相似三角形的相似比,可得 ,而要求
,而要求 ,需分类讨论,临界点为
,需分类讨论,临界点为 ,所以分成
,所以分成 和
和 分别求解,最后写成分段函数即可;(3)同(2),仍需要分成
分别求解,最后写成分段函数即可;(3)同(2),仍需要分成 和
和 分别讨论,而在每一种情况下还需要对等腰三角形哪两边相等进行分类讨论.
分别讨论,而在每一种情况下还需要对等腰三角形哪两边相等进行分类讨论.
试题解析:(1) 、
、 关于点
关于点 成中心对称,
成中心对称,
 ,
,


 ∽
∽
(2)①如图, 当
当 时,
时, ,由相似得
,由相似得
此时
②如图, 当
当 时,
时, ,由相似得
,由相似得
此时
 关于
关于 的函数解析式为
的函数解析式为 .
.
(3)①如图, 当
当 时,
时,
Ⅰ)若 ,
, 由相似得
由相似得 ,又
,又 ,
,
 ;
;
Ⅱ) ,显然
,显然 、
、 不可能;
不可能;
②如图, 当
当 时,
时,
Ⅰ)若 ,
, 由相似得
由相似得 ,又
,又 ,
,
 ;
;
Ⅱ)若 ,此时点
,此时点 、
、 分别与
分别与 、
、 重合,
重合, ;
;
Ⅲ)若 ,则
,则 ∽
∽ ,
, ,
, ,
,
综上,当 或
或 或
或 或
或 时,
时, 是等腰三角形.
是等腰三角形.
考点:1.相似三角形的判定及性质;2.点对称的性质;3. 分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,那么
,那么 等于 .
等于 . 元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,价格连续两次下调后,以每千克
元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,价格连续两次下调后,以每千克 元的单价对外批发销售.
元的单价对外批发销售. 吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:在原下调后价格的基础上,再次以相同的百分率降价;方案二:不打折,每吨优惠现金
吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:在原下调后价格的基础上,再次以相同的百分率降价;方案二:不打折,每吨优惠现金 元.试问小刘选择哪种方案更优惠,请说明理由.
元.试问小刘选择哪种方案更优惠,请说明理由. 中,点
中,点 是
是 边的中点,且
边的中点,且 //
// ,则
,则 ___________.
___________. 
 的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知
的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知 ,⊙O的半径为12,弧DE的长度为
,⊙O的半径为12,弧DE的长度为 .
.
 ,
, ,
, 作一圆弧,点
作一圆弧,点
 B.点
B.点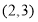 C.点
C.点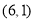 D.点
D.点