题目内容
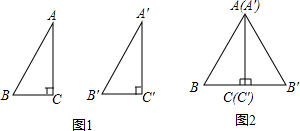
已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A′B′,AC=A′C′,C=∠C′=90°
求证:Rt△ABC和Rt△A′B′C′全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A′重合,点C与点C′重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.
求证:Rt△ABC和Rt△A′B′C′全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A′重合,点C与点C′重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

考点:直角三角形全等的判定,命题与定理
专题:
分析:(1)把已知的条件用语言叙述是一个直角三角形的斜边和一条直角边与另一个直角三形的斜边和一条直角边分别相等,结论是两个三角形全等,据此即可写出;
(2)分点A与点A′重合,点C与点C′重合两种情况即可作出图形;
(3)图②中,连接CC',利用等腰三角形中,等边对等角,即可证得∠BCC'=∠BCC',从而证得AC=A'C',然后利用SSS证明三角形全等.
(2)分点A与点A′重合,点C与点C′重合两种情况即可作出图形;
(3)图②中,连接CC',利用等腰三角形中,等边对等角,即可证得∠BCC'=∠BCC',从而证得AC=A'C',然后利用SSS证明三角形全等.
解答:解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
(2)如图:
 ;
;
图②使点A与点A'重合,点B与点B'重合
图③使点A与B'重合,B与点A’重合.
(3)在图②中,∵A和A'重合,B和B'重合,连接CC'.
∵∠ACB=∠A'C'B'=90°,∠ACB-∠ACC'=∠A'C'B'-∠AC'C,
即∠BCC'=∠BCC',
∴BC=B'C'.
在直角△ABC和直角△A'B'C'中,
,
∴△ABC≌△A'B'C'(SSS).
(2)如图:
 ;
;图②使点A与点A'重合,点B与点B'重合
图③使点A与B'重合,B与点A’重合.
(3)在图②中,∵A和A'重合,B和B'重合,连接CC'.
∵∠ACB=∠A'C'B'=90°,∠ACB-∠ACC'=∠A'C'B'-∠AC'C,
即∠BCC'=∠BCC',
∴BC=B'C'.
在直角△ABC和直角△A'B'C'中,
|
∴△ABC≌△A'B'C'(SSS).
点评:本题考查了直角三角形的全等中HL定理的证明,正确利用等腰三角形的性质是关键.

练习册系列答案
相关题目
新泰市某天的最高气温为6℃,最低气温为-9℃,那么这天的最高气温比最低气温高( )
| A、15℃ | B、-15℃ |
| C、3℃ | D、-3℃ |
下列方程中,是一元一次方程的是( )
| A、x2-4x=3 | ||
| B、x+2y=1 | ||
| C、x-1=0 | ||
D、x-1=
|
若圆的半径是5,圆心的坐标是(0,0),点P的坐标是(-4,3),则点P与⊙O的位置关系是( )
| A、点P在⊙O外 |
| B、点P在⊙O内 |
| C、点P在⊙O上 |
| D、点P在⊙O外或⊙O上 |
 如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )
如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )| A、28° | B、31° |
| C、32° | D、34° |
 如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.
如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.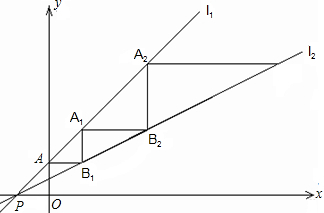 如图,直线l1:y=x+1与直线l2:y=
如图,直线l1:y=x+1与直线l2:y=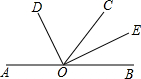 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.