��Ŀ����
����Ŀ��ij��˾����һ�ֽ�����Ʒ���г��Ϻ��ܻ�ӭ���ù�˾ÿ��IJ���Ϊ6��������ڹ��ں��������г�ȫ�����ۣ����ڹ������ۣ�ƽ��ÿ����Ʒ������y1��Ԫ�������������x��������ĺ�����ϵʽΪy1=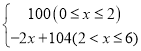 �����ڹ������ۣ�ƽ��ÿ����Ʒ������Ϊy2=84Ԫ��
�����ڹ������ۣ�ƽ��ÿ����Ʒ������Ϊy2=84Ԫ��
��1����ù�˾ÿ���ڹ��ں������۵�������w����Ԫ�������������x��������ĺ�����ϵʽ����ָ��x��ȡֵ��Χ��
��2���ù�˾ÿ���ڹ��ڹ�����������Ϊ����ʱ����ʹ��˾ÿ���������������ֵ�Ƕ��٣�
��3���ù�˾�ƻ��ӹ������۵�ÿ����Ʒ�о��2m��1��m��4��Ԫ��ϣ�����̣��ӹ������۵�ÿ����Ʒ�о��mԪ��ϣ�����̣��ҹ������۲�����4���������ʱ���ڹ������۵�����������ֵΪ520��Ԫ����m��ֵ��
���𰸡���1��w=![]() ����2�����ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ����3��m=2
����2�����ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ����3��m=2
��������
��1�����������ÿ����������Լ���������ֶκ�������ʽ������ɵý⣻
��2����ϣ�1���ֱ����ֶ������������ֵ�����ó����ֵ���ɣ�
��3���ù�˾�ƻ��ڹ������۲�����4��������ù�˾ÿ��������Ϊ6�������ù�˾ÿ���ڹ������۵ļ���x�ķ�ΧΪ��0��x��2����������w��=��100-2m��x����84-m����6-x��=��16-m��x��504-6m������m��ȡֵ��Χ��x��ȡֵ��Χ��һ�κ��������ʣ�������������Ϊ520��Ԫ���ɷ�����ã�
�⣺��1��w=y1x��84��6-x����
��0��x��2ʱ��w=100x��84��6-x��=16x��504��
��2��x��6ʱ��w=x��-2x��104����84��6-x��=-2x2��20x��504��
��w=![]() ��
��
��2����0��x��2ʱ��w=16x��504��
��k =16��0����x=2ʱ��w=16x��504�����ֵΪ536��
��2��x��6ʱ��w=-2x2��20x��504=-2��x-5��2��554��
��a=-2��0������x=5ʱȡ���ֵ554��
��554��536�����Ե�x=5ʱȡ���ֵ554��
�������ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ��
��3�����ù�˾�ƻ��ڹ������۲�����4�������6-x��4����x��2��
���ù�˾ÿ���ڹ������۵ļ���x�ķ�ΧΪ��0��x��2��
��������w��=��100-2m��x����84-m����6-x��=��16-m��x��504-6m��
��1��m��4����16-m��0����x=2ʱ��w��ȡ�����ֵ��
������ã�2��16-m����504-6m=536-8m=520����ã�m=2��