题目内容
【题目】如图,在 ![]() 中,
中, ![]() ,以
,以 ![]() 的中点
的中点 ![]() 为圆心分别与
为圆心分别与 ![]() ,
, ![]() 相切于
相切于 ![]() ,
, ![]() 两点,则
两点,则 ![]() 的长为( )
的长为( )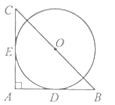
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】连接OE,OD,OA,∵以 B C 的中点 O 为圆心分别与 A B , A C 相切于 D , E 两点,
∴OD⊥AB,OE⊥AC;又∵ ∠ A = 90 °
∴四边形ADOE为矩形,又∵OE=OD
∴矩形ADOE为正方形;∠OAD=45°,OD⊥AB
∵OA=![]() BC=OB=
BC=OB=![]()
∴∠AOB=90° AB=![]() =2
=2
∴OD=![]() AB=1
AB=1
弧E D 的长为![]() =
=![]()
由两条切线以及∠A=90°易得四边形ADOE为矩形∠OAD=45°,再由直角三角形斜边上的中线等于斜边的一半易得OA=![]() BC=OB=
BC=OB=![]() 再由勾股定理,求得AB的长,从而得到OD=
再由勾股定理,求得AB的长,从而得到OD=![]() AB=1再利用弧长公式可得结果。
AB=1再利用弧长公式可得结果。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目