Question

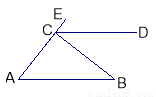
如图，正方形ABCD的边长是4cm，点G在边AB上，以BG为边向外作正方形GBFE，连接AE、AC、CE，则△AEC的面积是 cm2。

 

 

Answer 1

8

【解析】

试题分析：如图，把图形补全成矩形，设正方形GBFE的边长为x，求出矩形HFCD的面积等于4（x+4），再求出△EFC、△ACD、△AHE的面积分别为x（x+4）、×4×4、x（4﹣x），△AEC的面积等于矩形HFCD的面积减去△EFC、△ACD、△AHE的面积，整理即可。

如图，图形补全成矩形HFCD，设正方形GBFE的边长为x，则

S矩形HFCD=4（x+4），S△EFC=x（x+4）、S△ACD=×4×4、S△AHE=x（4﹣x），

∵△AEC的面积=S矩形HFCD﹣S△EFC﹣S△ACD﹣S△AHE，

=4（x+4）﹣x（x+4）﹣×4×4﹣x（4﹣x），

=4x+8﹣x（x+4+4﹣x），

=8cm2。

故答案为：8

考点：1.正方形的性质；2.三角形的面积。